Optimizers in deep learning
Gradient descent and its many variations are the de facto algorithms to optimize modern deep learning models. Deep learning libraries offers a multitude of these optimization algorithms and often remain enigmatic to most users and are treated as black boxes due to a lack of accessible explanations.
Gradient descent is one of the most popular algorithms to perform optimization and the de facto method to optimize neural networks. Every state-of-the-art deep learning library contains implementations of various algorithms to improve on vanilla gradient descent. These algorithms, however, are often used as black-box optimizers, as practical explanations are hard to come by.
This article aims at providing the reader with intuitions with regard to the behaviour of different algorithms for optimizing gradient descent.
Taking a step back: Gradient descent is a way to minimize an objective function $J(\theta)$ parameterized by a model's parameters $\theta \in \mathbb{R}^d$ by updating the parameters in the opposite direction of the gradient of the objective function $\nabla_\theta J(\theta)$ w.r.t. to the parameters. The learning rate $\eta$ determines the size of the steps we take to reach a (local) minimum. In other words, we follow the direction of the slope of the surface created by the objective function downhill until we reach a valley. This article discuss various methods to improve on this "blind" stepwise approach to following the slope.
Feel free to review previous articles if you need to brush up on computing partial derivatives, the gradient, gradient descent, regularization, and automatic differentiation (part1 and part 2).
We are going to cover the following optimizers in this article:
| Name | Description | TensorFlow Function | PyTorch Function |
|---|---|---|---|
| SGD | Stochastic Gradient Descent | tf.keras.optimizers.SGD |
torch.optim.SGD |
| Momentum | Stochastic Gradient Descent with Momentum | tf.keras.optimizers.SGD |
torch.optim.SGD |
| Nesterov | Nesterov Accelerated Gradient | tf.keras.optimizers.SGD |
torch.optim.SGD |
| Adam | Adaptive Moment Estimation | tf.keras.optimizers.Adam |
torch.optim.Adam |
| RMSprop | Root Mean Square Propagation* | tf.keras.optimizers.RMSprop |
torch.optim.RMSprop |
| Adagrad | Adaptive Gradient Algorithm | tf.keras.optimizers.Adagrad |
torch.optim.Adagrad |
| Adadelta | Adaptive Delta Learning | tf.keras.optimizers.Adadelta |
torch.optim.Adadelta |
| Adamax | Adaptive Moment Estimation with Infinity Norm | tf.keras.optimizers.Adamax |
torch.optim.Adamax |
| Nadam | Combination of Adam and Nesterov Momentum | tf.keras.optimizers.Nadam |
torch.optim.Nadam |
| AdamW | Adam with Weight Decay | tf.keras.optimizers.AdamW |
torch.optim.AdamW |
*Unpublished work by Geoff Hinton
Introduction
Stochastic Gradient Descent (SGD) is a widely-used optimization algorithm in machine learning and general optimization problems. It operates by iteratively updating the parameters of a model to minimize (or maximize) an objective function. At each iteration, SGD computes the gradient of the objective function with respect to the parameters, indicating the direction of steepest descent. Mathematically, this is represented as:
$$\text{gradient}_t = \nabla f(\text{parameters}_t)$$
Where $\text{gradient}_t$ is the gradient at iteration $t$, $f$ is the objective function, and $\text{parameters}_t$ are the parameters at iteration $t$.
The parameters are then updated using the gradient and a learning rate $\eta$. which controls the size of the updates:
$$\text{parameters}_{t+1} = \underbrace{\text{parameters}_t}_{\text{Current estimate}} - \overbrace{\eta \times \text{gradient}_t}^{\text{Take a step in the direction of the gradient}}$$
Consistency of symbols and language
To be consistent throughout this article, we will use $\theta$ for parameters, $\nabla f(\theta)$ for the gradient, a given iteration $t$, and the learning rate $\eta$. Rewriting the above equation with these symbols:
$$\theta_{t+1} = \theta_t - \eta\nabla f(\theta_t)$$
Consistency in implementation
To ensure a fair comparison between optimization methods, we will utilize Beale's function with three distinct initial positions. Beale's function is defined as:
$$f(x, y) = (1.5 - x + xy)^2 + (2.25 - x + xy^2)^2 + (2.625 - x + xy^3)^2$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = 2(1.5 - x + xy)(-1 + y) + 2(2.25 - x + xy^2)(-1 + y^2) + 2(2.625 - x + xy^3)(-1 + y^3)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = 2(1.5 - x + xy)x + 2(2.25 - x + xy^2)(2xy) + 2(2.625 - x + xy^3)(3xy^2)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Here is the function and its gradient in Python:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
# Define the Beale function
def beale(x, y):
return (1.5 - x + x * y)**2 + (2.25 - x + x * y**2)**2 + (2.625 - x + x * y**3)**2
# Define the gradient of the Beale function
def beale_gradient(x, y):
df_dx = 2 * (1.5 - x + x * y) * (-1 + y) + 2 * (2.25 - x + x * y**2) * (-1 + y**2) + 2 * (2.625 - x + x * y**3) * (-1 + y**3)
df_dy = 2 * (1.5 - x + x * y) * x + 4 * (2.25 - x + x * y**2) * x * y + 6 * (2.625 - x + x * y**3) * x * y**2
return np.array([df_dx, df_dy])SGD with Momentum
SGD encounters challenges when navigating ravines, regions where the terrain sharply inclines in one direction compared to others, commonly found near local optima. In such landscapes, SGD tends to oscillate along the steep slopes of the ravine, progressing hesitantly along the valley floor toward the local optimum.
Momentum, a technique aimed at improving on SGD, addresses these issues by accelerating the optimization process in the pertinent direction while mitigating oscillations. It achieves this by incorporating a fraction $\gamma$ of the update vector from the previous time step into the current update vector.
In essence, momentum is used exactly as you would think. Imagine a ball rolling down a slope. As the ball descends, it accumulates momentum, gradually increasing in speed (until it reaches its terminal velocity, accounting for air resistance, where $\gamma < 1$). Exactly like this, our parameter updates mimic this behavior: the momentum term amplifies for dimensions with consistent gradient directions, facilitating quicker convergence, while it dampens updates for dimensions with fluctuating gradient directions, thereby reducing oscillation. Consequently, momentum facilitates swifter convergence and diminished oscillatory behavior.
Mathematical Description
Mathematically, at each iteration of SGD with momentum (SGDM), the velocity of parameter updates is computed by adding a fraction $\gamma$ of the previous velocity to the current gradient multiplied by the learning rate:
$$v_{t+1} = \gamma \times v_t - \eta \nabla f(\theta_t)$$
$$\theta_{t+1} = \theta_t + v_{t+1}$$
Where $v_{t+1}$ is the velocity at iteration $t+1$ and $\gamma$ is the momentum parameter (typically between 0 and 1).

Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using SGD with momentum. The loss function is:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$ and momentum hyperparameter $\gamma = 0.9$. We initialize the model parameters $w_0 = w_1 = 0$, and set the initial velocity $v_0 = 0$.
The first iteration:
$$v_1 = \gamma v_0 - \eta \nabla f(w_0) = 0 - 0.01 [-10, -8] = [0.1, 0.08]$$
$$w_1 = w_0 + v_1 = [0, 0] + [0.1, 0.08] = [0.1, 0.08]$$
The second iteration:
$$v_2 = \gamma v_1 - \eta \nabla f(w_1) = 0.9 [0.1, 0.08] - 0.01 [-10, -8] = [0.19, 0.16]$$
$$w_2 = w_1 + v_2 = [0.1, 0.08] + [0.19, 0.16] = [0.29, 0.24]$$
And so on.
Advantages and Disadvantages over SGD
SGDM has several advantages over the original SGD algorithm:
- Faster Convergence: SGDM can converge faster than SGD, especially for non-convex optimization problems.
- Robustness to Local Minima: The momentum term helps to escape local minima, making it more robust to the optimization process.
- Handling Non-Convex Optimization Problems: Momentum is well-suited for handling non-convex optimization problems, which are common in deep learning.
However, SGDM also has some disadvantages:
- Computational Complexity: SGDM requires additional computations compared to SGD, making it more computationally expensive.
- Sensitivity to Hyperparameters: The momentum coefficient $\gamma$ can require careful tuning to achieve optimal performance.
- Memory Requirements: SGDM requires storing the velocity vector $v_t$, which can increase memory requirements.
Implementing SGD with Momentum from scratch in Python
# SGD with momentum optimizer implementation
def sgd_with_momentum_optimizer(func, grad_func, initial_params, learning_rate=0.01, momentum=0.9, max_iter=25000, tol=1e-6):
params = initial_params
velocity = np.zeros_like(params)
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
velocity = momentum * velocity - learning_rate * gradient
params += velocity
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
if t % 100 != 0:
params_history.append(params.copy())
print("Converged after", t, "iterations")
return params, params_history, tSGD with Nesterov accelerated gradient (NAG)
In momentum example above, we envisioned a ball rolling down a landscape without foresight. Instead, we want to to develop a more intuitive approach: a "smarter" ball that anticipates its trajectory and preemptively adjusting its speed before encountering an incline.
NAG imbues our momentum term with this foresight, providing a glimpse into the future position of the parameters. When utilizing the momentum term $\gamma v_{t-1}$ to update the parameters $\theta$, calculating $\theta - \gamma v_{t-1}$ yields an approximation of the forthcoming parameter position (albeit without considering the gradient for the complete update)(See Figure below). This approximation is akin to peering ahead on the hill's slope, providing a rough trajectory of our parameters' movement. Consequently, we effectively "look ahead" by computing the gradient not with respect to our current parameters $\theta$ but concerning the estimated future parameter position.


Mathematical Formulation
The mathematical formulation of Nesterov's Accelerated Gradient can be expressed as follows:
$$\theta_{k+1} = y_k - \eta \nabla f(y_k)$$
where $y_k$ is an intermediate point, $\eta$ is the learning rate, and $\nabla f(y_k)$ is the gradient of the loss function at $y_k$. The intermediate point $y_k$ is computed as:
$$y_k = \theta_k + \overbrace{\frac{\eta}{\sqrt{m}} \underbrace{(\theta_k - \theta_{k-1})}_{\substack{\text{current }\theta \\ \text{ minus previous }\theta}}}^{\substack{\text{Add in a fraction of the previous} \\ \text{estimate of the parameters }\theta}}$$
where $m$ is a parameter that controls the amount of acceleration. Dividing the learning rate by $\sqrt{m}$ helps in adjusting the step size based on the magnitude of the historical gradients.
$$m = \overbrace{\sum_i^{k+1} \nabla f(y_i)^2}^{\text{Sum of gradients squared}}$$
When the historical gradients are large, the learning rate is effectively reduced (since $m$ grows and thus $\eta/m$ shrinks), preventing the optimizer from taking excessively large steps. Conversely, when the historical gradients are small, the learning rate increases, allowing the optimizer to make more substantial progress.
Note that $m$ is a vector of the same size as $\theta$, and thus scale the learning rate differently for each parameter $\theta$ proportionally to the gradients observed thus far. In our example use-case with the Beale function $f(x,y)$ then both $\theta$ and $m$ are 2-dimensional vectors ($m \in \mathbb{R}^{2})$
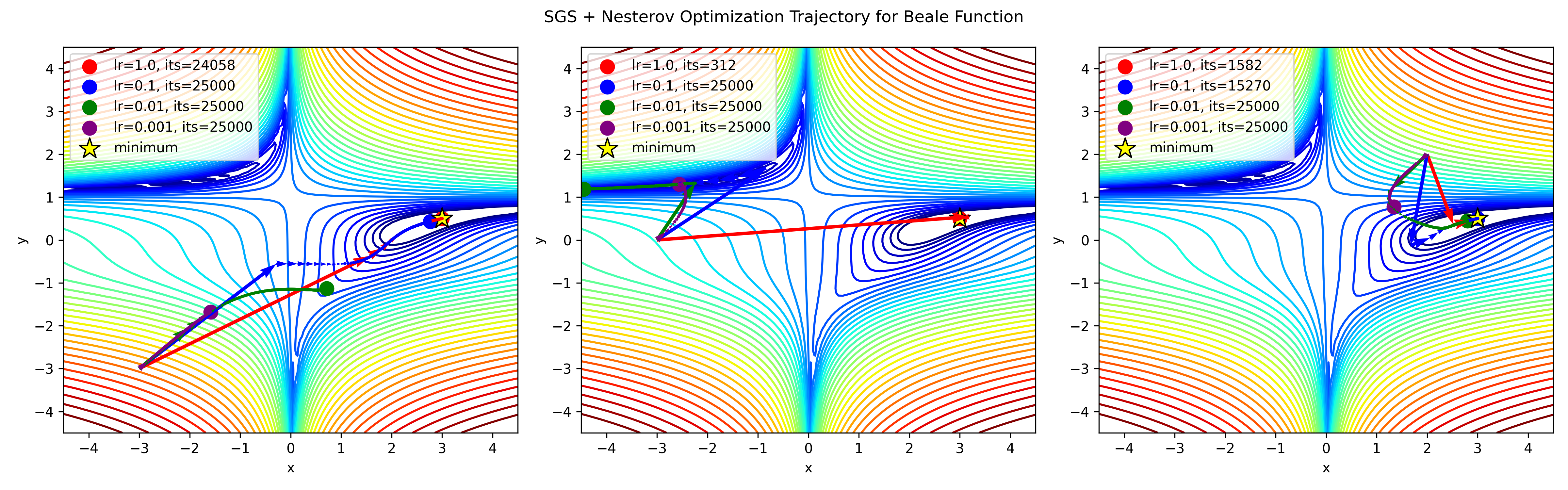
Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using SGD with Nesterov. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$ and momentum hyperparameter $\gamma = 0.9$. We initialize the model parameters $w_0 = w_1 = 0$, and set the initial velocity $v_0 = 0$.
The first iteration:
$$v_1 = \gamma v_0 - \eta \nabla f(w_0 + \gamma v_0) = 0 - 0.01 [-10, -8] = [0.1, 0.08]$$
$$w_1 = w_0 + v_1 = [0, 0] + [0.1, 0.08] = [0.1, 0.08]$$
The second iteration:
$$v_2 = \gamma v_1 - \eta \nabla f(w_1 + \gamma v_1) = 0.9 [0.1, 0.08] - 0.01 [-10, -8] = [0.19, 0.16]$$
$$w_2 = w_1 + v_2 = [0.1, 0.08] + [0.19, 0.16] = [0.29, 0.24]$$
And so on.
Advantages and Disadvantages over SGD
The Nesterov optimizer has several advantages over SGD:
- Convergence speed: The Nesterov optimizer converges faster than SGD, especially for non-convex optimization problems.
- Robustness to local minima: The Nesterov optimizer is more robust to local minima than SGD, which can get stuck in poor local optima.
However, the Nesterov optimizer also has some disadvantages:
- Computational complexity: The Nesterov optimizer requires more computational resources than SGD, especially for large datasets. NAG requires storing the intermediate points $y_k$ and previous estimates $\theta_{k-1}$, which can be memory-intensive for large models.
- Sensitivity to hyperparameters: The Nesterov optimizer is sensitive to hyperparameters such as the learning rate and the step size, which can be difficult to tune. NAG is sensitive to the choice of learning rate and acceleration parameter $m$, which can affect its performance.
Implementing SGD with Nesterov Accelerated Gradient from scratch in Python
# Nesterov optimizer implementation
def nesterov_optimizer(func, grad_func, initial_params, learning_rate=0.01, momentum=0.9, eps=1e-8, max_iter=25000, tol=1e-6):
params = initial_params
velocity = np.zeros_like(params)
m = np.zeros_like(params) # Historical gradient sum
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
lookahead_params = params - momentum * velocity
gradient = grad_func(*lookahead_params)
m += gradient ** 2
adjusted_learning_rate = learning_rate / np.sqrt(m + eps)
velocity = momentum * velocity + adjusted_learning_rate * gradient
params -= velocity
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
print("Converged after", t, "iterations")
# print(t, 'm', m)
return params, params_history, tAdaptive Moment Estimation (Adam)
Adam is an optimization method that dynamically adjusts learning rates for each parameter during training. Adam maintains two exponentially decaying averages: $m_t$, representing the first moment (mean) of the gradients, and $v_t$, representing the second moment (uncentered variance) of the gradients. This approach allows Adam to adaptively scale the learning rates based on the gradients' magnitude and variance, hence its name.
However, the initial estimates of $m_t$ and $v_t$ are biased towards zero, especially during the early stages of training and when the decay rates $\beta_1$ and $\beta_2$ are close to 1. To mitigate these biases, Adam computes bias-corrected estimates $\hat{m}_t$ and $\hat{v}_t$ by dividing the moment estimates by a term that accounts for the decay rates and the iteration number. These bias-corrected estimates are then used to update the parameters.
The update rule of Adam combines the bias-corrected estimates to adjust the parameters accordingly. The authors of Adam recommend default values of $\beta_1 = 0.9$, $\beta_2 = 0.999$, and $\epsilon = 10^{-8}$ for numerical stability. Empirical studies have demonstrated that Adam performs effectively in practice and often outperforms other adaptive learning algorithms.
Taken together, Adam incorporates two main ideas:
- Adaptive learning rate: Adam adjusts the learning rate for each parameter based on its previous updates, allowing it to adapt to different regions of the loss landscape.
- Momentum term: Adam incorporates a momentum-like term that helps the optimizer escape local minima and improves convergence.
Mathematical Formulation
The mathematical formulation of Adam can be written as follows:
$$m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla f(\theta_t)$$
$$v_t = \beta_2 v_{t-1} + (1-\beta_2) (\nabla f(\theta_t))^2$$
$$\theta_t = \theta_{t-1} - \eta \frac{m_t}{\sqrt{v_t}+\epsilon}$$
where:
- $m_t$ and $v_t$ are the first and second moments of the gradients, respectively
- $\beta_1$ and $\beta_2$ are hyperparameters that control the exponential decay rates of the moments (usually set to 0.9 and 0.999)
- $\epsilon$ is a small value added for numerical stability
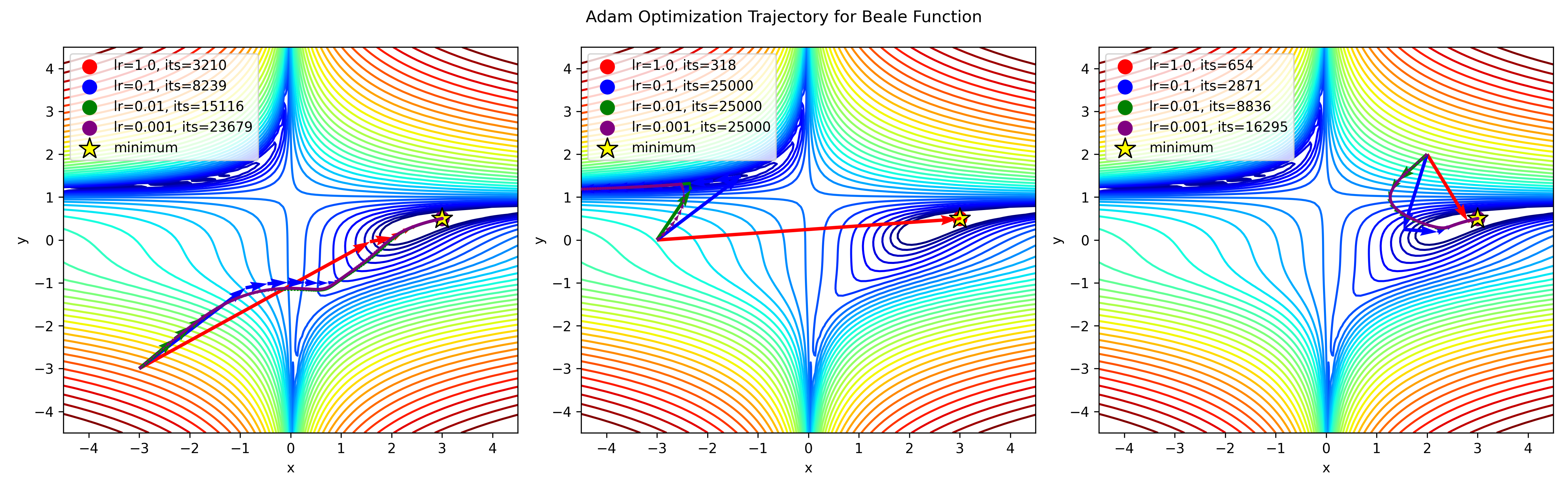
Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using Adam. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$, $\beta_1 = 0.9$, $\beta_2 = 0.999$, and $\epsilon = 1e-8$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial velocity $m_0 = v_0 = 0$.
The first iteration:
$$m_1 = \beta_1 m_0 + (1 - \beta_1) \nabla f(w_0) = 0.9 \times 0 + (1 - 0.9) \times [-10, -8] = [0.1, 0.08]$$
$$v_1 = \beta_2 v_0 + (1 - \beta_2) \nabla f(w_0)^2 = 0.999 \times 0 + (1 - 0.999) \times [100, 64] = [0.1, 0.08]$$
$$m_1^{corrected} = \frac{m_1}{1 - \beta_1} = \frac{[0.1, 0.08]}{1 - 0.9} = [1, 0.8]$$
$$v_1^{corrected} = \frac{v_1}{1 - \beta_2} = \frac{[0.1, 0.08]}{1 - 0.999} = [100, 64]$$
$$w_1 = w_0 - \eta \times \frac{m_1^{corrected}}{\sqrt{v_1^{corrected}} + \epsilon} = [0, 0] - 0.01 \times \frac{[1, 0.8]}{\sqrt{[100, 64]} + 1e-8}$$
The second iteration:
$$m_2 = \beta_1 m_1 + (1 - \beta_1) \nabla f(w_1) = 0.9 \times [0.1, 0.08] + (1 - 0.9) \times [-10, -8]$$
$$v_2 = \beta_2 v_1 + (1 - \beta_2) \nabla f(w_1)^2 = 0.999 \times [0.1, 0.08] + (1 - 0.999) \times [100, 64]$$
$$m_2^{corrected} = \frac{m_2}{1 - \beta_1^2} = \frac{[0.19, 0.16]}{1 - 0.9^2}$$
$$v_2^{corrected} = \frac{v_2}{1 - \beta_2^2} = \frac{[0.19, 0.16]}{1 - 0.999^2}$$
$$w_2 = w_1 - \eta \times \frac{m_2^{corrected}}{\sqrt{v_2^{corrected}} + \epsilon}$$
And so on.
Implementing Adam from scratch in Python
# Adam optimizer implementation
def adam_optimizer(func, grad_func, initial_params, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8, max_iter=25000, tol=1e-6):
params = initial_params
m = np.zeros_like(params)
v = np.zeros_like(params)
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
m = beta1 * m + (1 - beta1) * gradient
v = beta2 * v + (1 - beta2) * (gradient ** 2)
m_hat = m / (1 - beta1**t)
v_hat = v / (1 - beta2**t)
params -= learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
if t % 100 != 0:
params_history.append(params.copy())
print("Converged after", t, "iterations")
return params, params_history, tRMSprop
RMSprop and Adadelta were developed independently during the same period, driven by the necessity to address Adagrad's issue of drastically diminishing learning rates over time. In fact, RMSprop's initial update vector is identical to the one derived for Adadelta, as outlined in that section.
Both RMSprop and Adadelta were proposed as solutions to address Adagrad's problem of overly diminishing learning rates. Despite their independent development, they share a common objective: to effectively adapt the learning rate during training to ensure convergence without the constraints posed by Adagrad's cumulative gradient accumulation.
Mathematical Formulation
The RMSprop update rule is as follows:
$$v_t = \beta v_{t-1} + (1 - \beta)(\nabla f(\theta_t))^2$$
$$\theta_t = \theta_{t-1} - \eta \frac{\nabla f(\theta_t)}{\sqrt{v_t} + \epsilon}$$
$v_t$ denotes RMSprop's "moving" average of the squared gradients. It is also updated using an exponentially weighted moving average of the squared gradients.
$\beta$ is a hyperparameter that controls the decay rate of the moving average. Typically, it is set to a value close to 1 (e.g., 0.9 or 0.99).
$\epsilon$ is a small constant added to the denominator for numerical stability, preventing division by zero.
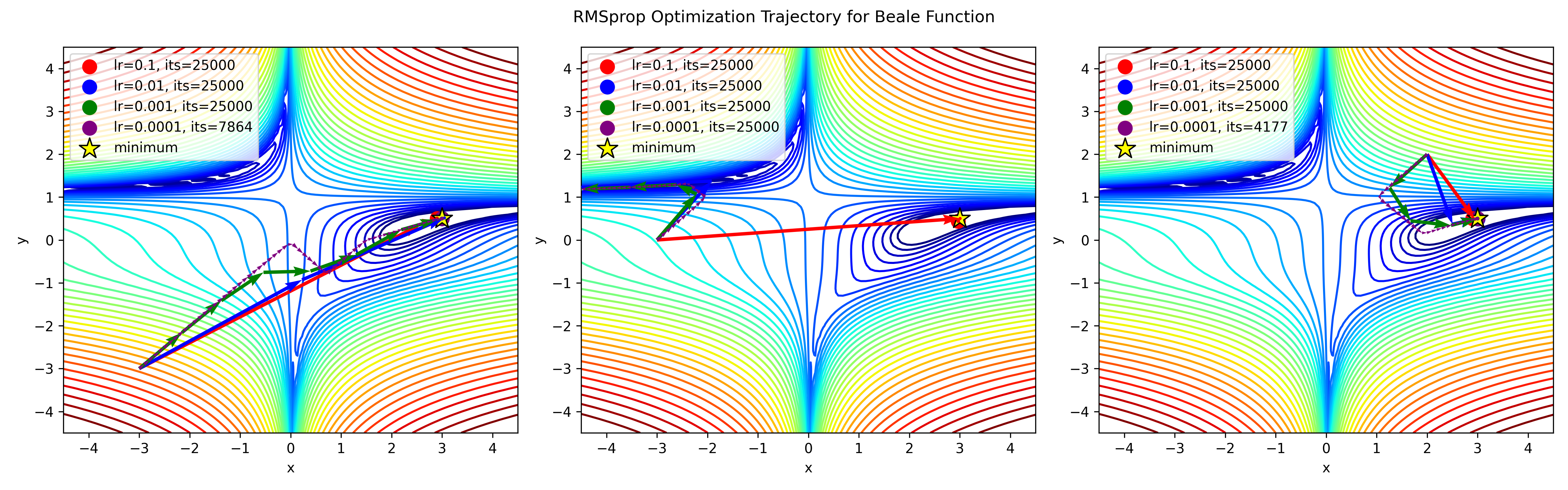
Concrete example
Suppose we have a neural network with two layers, and we want to optimize its parameters using RMSprop. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$ and decay rate $\rho = 0.9$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial accumulated squared gradient $v_0 = 0$.
The first iteration:
$$v_1 = \rho v_0 + (1 - \rho) (\nabla f(w_0))^2 = 0.9 \times 0 + (1 - 0.9) \times [100, 64] = [10, 6.4]$$
$$w_1 = w_0 - \frac{\eta}{\sqrt{v_1} + \epsilon} \cdot \nabla f(w_0) = [0, 0] - \frac{0.01}{\sqrt{[10, 6.4]} + \epsilon} \cdot [-10, -8]$$
The second iteration:
$$v_2 = \rho v_1 + (1 - \rho) (\nabla f(w_1))^2 = 0.9 \times [10, 6.4] + (1 - 0.9) \times [100, 64]$$
$$w_2 = w_1 - \frac{\eta}{\sqrt{v_2} + \epsilon} \cdot \nabla f(w_1)$$
And so on.
Implementing RMSprop from scratch in Python
# RMSprop optimizer implementation with momentum
def rmsprop_optimizer(func, grad_func, initial_params, learning_rate=0.01, decay_rate=0.9, momentum=0.9, eps=1e-8, max_iter=25000, tol=1e-6):
params = initial_params
velocity = np.zeros_like(params)
rmsprop_cache = np.zeros_like(params) # Cache for squared gradients
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
rmsprop_cache = decay_rate * rmsprop_cache + (1 - decay_rate) * gradient ** 2
adjusted_learning_rate = learning_rate / (np.sqrt(rmsprop_cache) + eps)
velocity = momentum * velocity - adjusted_learning_rate * gradient
params += velocity
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
print("Converged after", t, "iterations")
return params, params_history, t
Adagrad
Adagrad is an optimization algorithm designed to adapt the learning rate for each parameter individually based on the historical gradients observed during training. Unlike traditional optimization methods with a fixed learning rate, Adagrad dynamically adjusts the learning rate to perform larger updates for infrequent parameters and smaller updates for frequent parameters. This adaptability makes Adagrad well-suited for dealing with sparse data, where some parameters may have more influence than others.
The core idea behind Adagrad is to maintain a separate learning rate for each parameter, which is scaled inversely proportional to the square root of the sum of the squared gradients accumulated over time. Let's denote $m_t$ as the sum of squared gradients up to time step $t$ for parameter $\theta$:
$$m_t = m_{t-1} + (\nabla f(\theta_t))^2$$
The update rule for Adagrad can then be expressed as:
$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{m_t + \epsilon}} \nabla f(\theta_t)$$
In this equation, $\epsilon$ is a small constant added to the denominator to prevent division by zero. By scaling the learning rate inversely proportional to the square root of the accumulated squared gradients, Adagrad effectively reduces the learning rate for parameters that have experienced large gradients in the past, thereby mitigating the risk of overshooting the optimal solution.
However, one drawback of Adagrad is its tendency to accumulate the squared gradients in the denominator, leading to a monotonically decreasing learning rate over time. This diminishing learning rate can eventually become too small, hindering further learning progress. To address this issue, subsequent optimization algorithms such as RMSprop, Adadelta, and Adam have been developed to provide more robust and stable learning rate adaptation.
Mathematical Formulation
The mathematical formulation of Adagrad is given by:
$$\theta_t = \theta_{t-1} - \eta_t \nabla_\theta J(\theta)$$
The learning rate at iteration $t$, $\eta_t$, is calculated as:
$$\eta_t = \frac{\eta_0}{\sqrt{\sum_{i=1}^t g_i^2}}$$
where $g_i$ represents the gradient magnitude at iteration $i$, and $\eta_0$ is the initial learning rate.
The second term highlights the primary drawback of Adagrad with its accumulation of squared gradients in the denominator. As each term added to the sum is positive, the cumulative total grows continuously during training. Consequently, the learning rate diminishes over time, eventually reaching minuscule values where the algorithm's capacity to further improve becomes severely limited.

Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using Adagrad. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial accumulated squared gradient $G_0 = 0$.
The first iteration:
$$G_1 = G_0 + (\nabla f(w_0))^2 = 0 + [100, 64] = [100, 64]$$
$$w_1 = w_0 - \frac{\eta}{\sqrt{G_1} + \epsilon} \cdot \nabla f(w_0) = [0, 0] - \frac{0.01}{\sqrt{[100, 64]} + \epsilon} \cdot [-10, -8]$$
The second iteration:
$$G_2 = G_1 + (\nabla f(w_1))^2 = [100, 64] + [100, 64]$$
$$w_2 = w_1 - \frac{\eta}{\sqrt{G_2} + \epsilon} \cdot \nabla f(w_1)$$
And so on.
Implementing Adagrad from scratch in Python
def adagrad_optimizer(func, grad_func, initial_params, learning_rate=0.01, epsilon=1e-8, max_iter=20000, tol=1e-6):
params = initial_params
grad_squared_sum = np.zeros_like(params)
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
grad_squared_sum += gradient ** 2
adjusted_learning_rate = learning_rate / (np.sqrt(grad_squared_sum) + epsilon)
params -= adjusted_learning_rate * gradient
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
if t % 100 != 0:
params_history.append(params.copy())
print("Converged after", t, "iterations")
return params, params_history, tAdadelta
Adadelta is an optimization algorithm that addresses the limitations of Adagrad, particularly its tendency to diminish the learning rate over time due to the accumulation of squared gradients in the denominator. Adadelta improves upon Adagrad by restricting the accumulation of past gradients to a fixed-size window, thereby preventing the learning rate from monotonically decreasing.
Instead of storing all past squared gradients, Adadelta maintains a decaying average of the squared gradients over time. This running average, denoted as $E[g^2]_t$ at time step $t$, is recursively defined as a fraction of the current gradient $g_t$ and the previous average. The update rule for $E[g^2]_t$ is given by:
$$E[g^2]t = \gamma E[g^2]{t-1} + (1 - \gamma) g^2_t$$
Here, $\gamma$ is a decay factor that controls the rate at which past gradients are forgotten. By updating $E[g^2]_t$ based on a decaying average, Adadelta effectively adapts the learning rate to the changing dynamics of the optimization process.
The parameters are then updated using the root mean square (RMS) of the parameter updates, denoted as $\Delta \theta_t$. This RMS value is computed as the square root of the running average of squared parameter updates $E[\Delta \theta^2]_t$ plus a small constant $\epsilon$ to ensure numerical stability:
$$\Delta \theta_t = -\frac{\sqrt{E[\Delta \theta^2]_{t-1} + \epsilon}}{\sqrt{E[g^2]_t + \epsilon}} g_t$$
The use of the RMS of parameter updates helps to mitigate the diminishing learning rate problem observed in Adagrad. Additionally, Adadelta does not require manually setting a global learning rate, making it more convenient to use in practice.
Overall, Adadelta provides a more robust and stable optimization method compared to Adagrad, making it well-suited for training deep neural networks and handling sparse data.
Mathematical Formulation
The mathematical formulation of Adadelta can be written as follows:
$$\theta_t = \theta_{t-1} - \eta \frac{\nabla f(\theta_{t-1})}{\sqrt{E[g^2]_t} + \epsilon}$$
where $\theta_t$ is the model parameter at time step $t$, $\nabla f(\theta)$ is the gradient of the loss function, $\eta$ is the learning rate, $g_t = \nabla f(\theta_{t-1})$ is the gradient at time step $t$, and $E[g^2]_t$ is the exponentially decaying average of squared gradients.
The update rule for Adadelta can be further broken down into two components:
$$\Delta\theta_t = - \eta \frac{\nabla f(\theta_{t-1})}{\sqrt{E[g^2]_t} + \epsilon}$$
and
$$E[g^2]t = \gamma E[g^2]{t-1} + (1-\gamma) g_t^2$$
where $\gamma$ is a decay rate, typically set to 0.9.
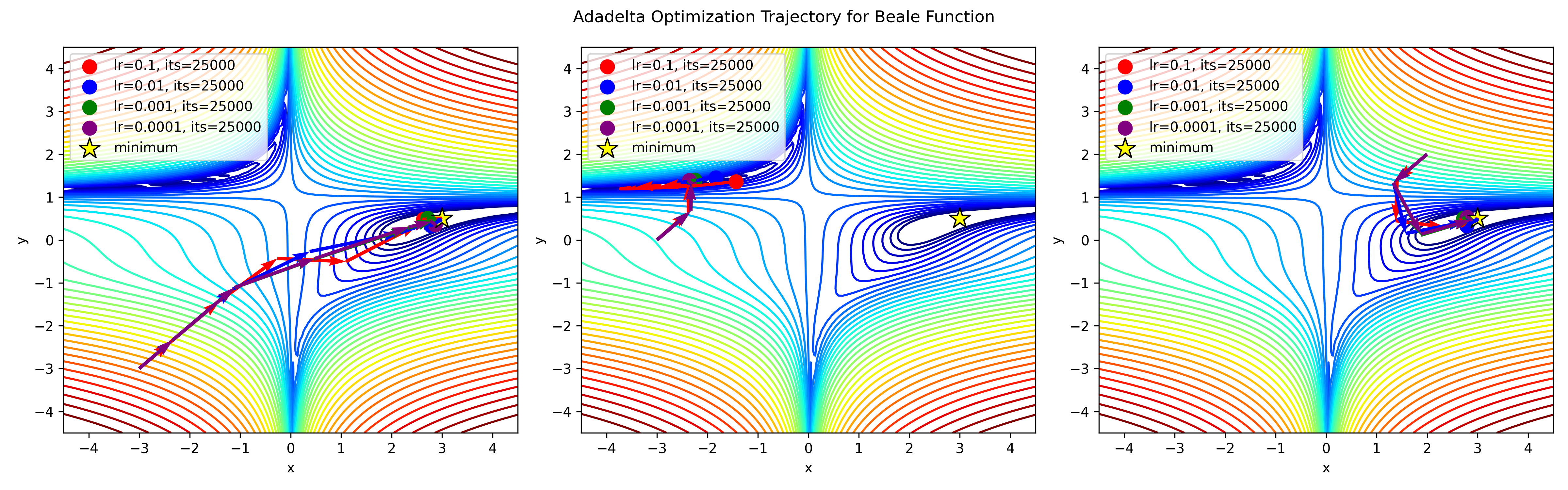
Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using Adadelta. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a decay rate $\rho = 0.9$ and a small constant $\epsilon = 1e-8$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial accumulated squared gradient $G_0 = 0$ and the initial accumulated squared update $\Delta w_0 = \Delta w_1 = 0$.
The first iteration:
$$G_1 = \rho G_0 + (1 - \rho) (\nabla f(w_0))^2 = 0.9 \times 0 + (1 - 0.9) \times [100, 64] = [10, 6.4]$$
$$\Delta w_1 = - \frac{\sqrt{\Delta w_0} + \epsilon}{\sqrt{G_1} + \epsilon} \cdot \nabla f(w_0) = - \frac{\sqrt{0} + 1e-8}{\sqrt{[10, 6.4]} + 1e-8} \cdot [-10, -8]$$
$$w_1 = w_0 + \Delta w_1$$
The second iteration:
$$G_2 = \rho G_1 + (1 - \rho) (\nabla f(w_1))^2$$
$$\Delta w_2 = - \frac{\sqrt{\Delta w_1} + \epsilon}{\sqrt{G_2} + \epsilon} \cdot \nabla f(w_1)$$
$$w_2 = w_1 + \Delta w_2$$
And so on.
Implementing Adadelta from scratch in Python
# Adadelta optimizer implementation
def adadelta_optimizer(func, grad_func, initial_params, rho=0.95, eps=1e-6, max_iter=25000, tol=1e-6):
params = initial_params
accumulated_gradient = np.zeros_like(params)
accumulated_delta = np.zeros_like(params)
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
accumulated_gradient = rho * accumulated_gradient + (1 - rho) * gradient ** 2
delta_params = -np.sqrt(accumulated_delta + eps) / np.sqrt(accumulated_gradient + eps) * gradient
params += delta_params
accumulated_delta = rho * accumulated_delta + (1 - rho) * delta_params ** 2
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
print("Converged after", t, "iterations")
return params, params_history, t
Adamax
AdaMax is an extension of the Adam optimization algorithm that introduces a new factor, $v_t$, in the update rule. This factor scales the gradient inversely proportional to the $L^p$ norm of the past gradients (via the $v_{t-1}$ term) and the current gradient $|g_t|^2$. While the original Adam algorithm employs the $L^2$ norm, AdaMax generalizes this concept to accommodate different norms, parameterized by $\beta_{p}^2$.
In practice, norms with large $p$ values tend to become numerically unstable. However, the $L^1$ and $L^2$ norms are commonly used due to their stability. Interestingly, the $L^{\infty}$ norm, which represents the maximum absolute value among the elements of a vector, also exhibits stable behavior. Leveraging this stability, the authors propose AdaMax, which constrains $v_t$ using the $L^{\infty}$ norm to ensure convergence to a more stable value.
To differentiate AdaMax from Adam and to denote the infinity norm-constrained $v_t$, we use $u_t$. This $u_t$ is computed as the maximum between $\beta_{\infty}^2 \cdot v_{t-1}$ and $|g_t|$. Unlike Adam, which requires bias correction for $m_t$ and $v_t$, AdaMax does not need such correction for $u_t$ due to its reliance on the maximum operation.
The AdaMax update rule replaces $\sqrt{\hat{v}_t + \epsilon}$ in the Adam update equation with $u_t$, resulting in a more robust optimization process. Default values for the hyperparameters, such as $\eta = 0.002$, $\beta_1 = 0.9$, and $\beta_2 = 0.999$, are commonly recommended for AdaMax.
Mathematical Formulation
The mathematical formulation of Adamax can be written as follows:
$$m_t = \beta_1 m_{t-1} + (1 - \beta_1) \nabla f(\theta_t)$$
$$v_t = \beta_2 v_{t-1} + (1 - \beta_2) (\nabla f(\theta_t))^2$$
$$\theta_t = \theta_{t-1} - \frac{\eta_t m_t}{\sqrt{v_t} + \epsilon}$$
where:
- $m_t$ is the first moment estimate
- $v_t$ is the second moment estimate
- $\beta_1$ and $\beta_2$ are hyperparameters controlling the decay rates of the moments
- $\eta_t$ is the adaptive learning rate at time step $t$
- $\epsilon$ is a small value for numerical stability
The update rules for Adamax iteratively adjust model parameters to minimize the loss function. The first moment estimate, $m_t$, captures the average gradient direction, while the second moment estimate, $v_t$, tracks the magnitude of the gradients. The adaptive learning rate, $\eta_t$, is calculated as:
$$\eta_t = \frac{\eta}{\sqrt{v_t} + \epsilon}$$
As in other optimizers we've seen so far, the momentum term, $m_t$, helps Adamax escape local minima by incorporating past gradient information.

Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using Adamax. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$, $\beta_1 = 0.9$, and $\beta_2 = 0.999$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial velocity $m_0 = v_0 = 0$.
The first iteration:
$$m_1 = \beta_1 m_0 + (1 - \beta_1) \nabla f(w_0) = 0.9 \times 0 + (1 - 0.9) \times [-10, -8] = [1, 0.8]$$
$$u_1 = \max(\beta_2 v_0, |\nabla f(w_0)|) = \max(0, |[-10, -8]|) = [10, 8]$$
$$w_1 = w_0 - \frac{\eta}{1 - \beta_1} \frac{m_1}{u_1} = [0, 0] - \frac{0.01}{1 - 0.9} \frac{[1, 0.8]}{[10, 8]}$$
The second iteration:
$$m_2 = \beta_1 m_1 + (1 - \beta_1) \nabla f(w_1) = 0.9 \times [1, 0.8] + (1 - 0.9) \times [-10, -8]$$
$$u_2 = \max(\beta_2 v_1, |\nabla f(w_1)|) = \max(0.9 [10, 8], |[-10, -8]|)$$
$$w_2 = w_1 - \frac{\eta}{1 - \beta_1} \frac{m_2}{u_2}$$
And so on.
Implementing Adamax from scratch in Python
# Adamax optimizer implementation
def adamax_optimizer(func, grad_func, initial_params, learning_rate=0.01, beta1=0.9, beta2=0.999, eps=1e-8, max_iter=25000, tol=1e-6):
params = initial_params
m = np.zeros_like(params) # Exponential moving average of gradient
u = np.zeros_like(params) # Exponential moving average of squared gradient with infinite norm
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
m = beta1 * m + (1 - beta1) * gradient
u = np.maximum(beta2 * u, np.abs(gradient))
params -= learning_rate / (1 - beta1**t) * m / (u + eps)
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
print("Converged after", t, "iterations")
return params, params_history, tNesterov-accelerated Adaptive Moment Estimation (Nadam)
Adam, as previously discussed, blends the attributes of RMSprop and momentum: RMSprop contributes the exponentially decaying average of past squared gradients $v_t$, while momentum accounts for the exponentially decaying average of past gradients $m_t$. In general, Nesterov accelerated gradient (NAG) outperforms vanilla momentum.
Nadam (Nesterov-accelerated Adaptive Moment Estimation), an enhancement over Adam, amalgamates the concepts of Adam and NAG. To integrate NAG into Adam, we need to adapt its momentum term $m_t$. Let's revisit the momentum update rule using our current notation:
$$g_t = \nabla_{\theta_t} J(\theta_t)$$
$$m_t = \gamma m_{t-1} + \eta g_t$$
$$\theta_{t+1} = \theta_t - m_t$$
This formula illustrates that momentum entails taking a step in the direction of the previous momentum vector and another step in the direction of the current gradient. NAG enhances this process by allowing a more accurate step in the gradient direction. This is achieved by updating the parameters with the momentum step before computing the gradient. We can achieve NAG by modifying the gradient $g_t$ as follows:
$$g_t = \nabla_{\theta_t} J(\theta_t - \gamma m_{t-1})$$
$$m_t = \gamma m_{t-1} + \eta g_t$$
$$\theta_{t+1} = \theta_t - m_t$$
To incorporate Nesterov momentum into Adam, we replace the previous momentum vector with the current momentum vector. Recall the Adam update rule:
$$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$$
$$\hat{m}t = \frac{m_t}{1 - \beta^t_1}$$
$$\theta{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t + \epsilon}} \hat{m}_t$$
Expanding the second equation with the definitions of $\hat{m}_t$ and $m_t$ gives us:
$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}t + \epsilon}} \left( \frac{\beta_1 m{t-1}}{1 - \beta^t_1} + \frac{(1 - \beta_1) g_t}{1 - \beta^t_1} \right)$$
Notice that $\frac{\beta_1 m_{t-1}}{1 - \beta^t_1}$ is the bias-corrected estimate of the momentum vector of the previous time step. We can replace it with $\hat{m}_{t-1}$:
$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}t + \epsilon}} \left( \hat{m}{t-1} + \frac{(1 - \beta_1) g_t}{1 - \beta^t_1} \right)$$
This equation closely resembles our expanded momentum term in the NAG formula (see above). We can add Nesterov momentum to Adam by simply replacing the bias-corrected estimate of the momentum vector of the previous time step $\hat{m}_{t-1}$ with the bias-corrected estimate of the current momentum vector $\hat{m}_t$, resulting in the Nadam update rule:
$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t + \epsilon}} \left( \beta_1 \hat{m}_t + \frac{(1 - \beta_1) g_t}{1 - \beta^t_1} \right)$$
Mathematical Formulation
The mathematical formulation of Nadam is based on the following equations:
$$m_t = \beta_1 m_{t-1} + (1-\beta_1) \nabla f(\theta_t)$$
$$v_t = \beta_2 v_{t-1} + (1-\beta_2) (\nabla f(\theta_t))^2$$
$$\theta_{t+1} = \theta_t - \eta \frac{m_t}{\sqrt{v_t} + \epsilon}$$
where:
- $\beta_1$ and $\beta_2$ are hyperparameters controlling the decay rates of the moving averages
- $\eta$ is the learning rate
- $\theta_t$ is the model parameter at iteration $t$
- $\epsilon$ is a small value to prevent division by zero
The Nadam optimizer iteratively updates the model parameters using the above equations, which adaptively adjust the step size based on the magnitude of the gradient and the second moment of the gradients.
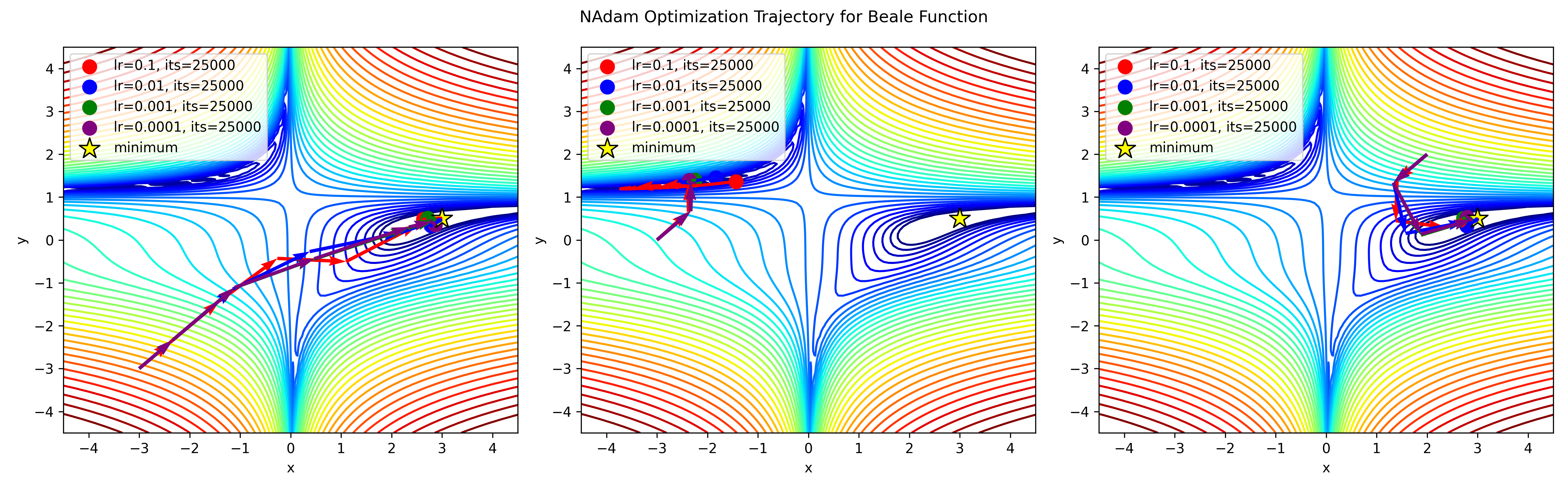
Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using NAdam. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$, $\beta_1 = 0.9$, $\beta_2 = 0.999$, and $\epsilon = 1e-8$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial velocity $m_0 = v_0 = 0$.
The first iteration:
$$m_1 = \beta_1 m_0 + (1 - \beta_1) \nabla f(w_0) = 0.9 \times 0 + (1 - 0.9) \times [-10, -8] = [1, 0.8]$$
$$v_1 = \frac{\beta_1 m_1 + (1 - \beta_1) \nabla f(w_0)}{1 - \beta_1} = \frac{0.9 [1, 0.8] + (1 - 0.9) \times [-10, -8]}{1 - 0.9}$$
$$w_1 = w_0 - \eta \frac{v_1}{\sqrt{\sum_{i=1}^{t} \beta_2^i}} = [0, 0] - 0.01 \frac{v_1}{\sqrt{\sum_{i=1}^{t} \beta_2^i}}$$
The second iteration:
$$m_2 = \beta_1 m_1 + (1 - \beta_1) \nabla f(w_1) = 0.9 [1, 0.8] + (1 - 0.9) \times [-10, -8]$$
$$v_2 = \frac{\beta_1 m_2 + (1 - \beta_1) \nabla f(w_1)}{1 - \beta_1}$$
$$w_2 = w_1 - \eta \frac{v_2}{\sqrt{\sum_{i=1}^{t} \beta_2^i}}$$
And so on.
Implementing Nadam from scratch in Python
# NAdam optimizer implementation
def nadam_optimizer(func, grad_func, initial_params, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8, max_iter=25000, tol=1e-6):
params = initial_params
m = np.zeros_like(params) # Exponential moving average of gradient
v = np.zeros_like(params) # Exponential moving average of squared gradient
t = 0
beta1_product = beta1
beta2_product = beta2
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
m = beta1 * m + (1 - beta1) * gradient
v = beta2 * v + (1 - beta2) * (gradient ** 2)
# Bias correction
m_hat = m / (1 - beta1_product)
v_hat = v / (1 - beta2_product)
# Update parameters
params -= learning_rate * m_hat / (np.sqrt(v_hat) + epsilon)
# Update beta1 and beta2 products
beta1_product *= beta1
beta2_product *= beta2
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
print("Converged after", t, "iterations")
return params, params_history, tAdamW
AdamW, similar to Adam, computes adaptive learning rates for each parameter by maintaining exponentially decaying averages of past gradients $m_t$ and squared gradients $v_t$. However, AdamW introduces weight decay to address the problem of weight magnitude growth during training. Weight decay, also known as L2 regularization, penalizes large parameter values by adding a term to the loss function proportional to the squared magnitude of the parameters.
The AdamW update rule modifies the original Adam update rule by incorporating weight decay directly into the parameter updates. Let's revisit the Adam update rule:
$$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$$
$$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$$
$$\hat{m}_t = \frac{m_t}{1 - \beta^t_1}$$
$$\hat{v}t = \frac{v_t}{1 - \beta^t_2}$$
$$\theta{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t + \epsilon}} \hat{m}_t$$
To incorporate weight decay, denoted by $\lambda$, into the Adam update rule, we adjust the parameter update step:
$$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t + \epsilon}} \hat{m}_t - \lambda \theta_t$$
This equation includes an additional term $-\lambda \theta_t$ to penalize large parameter values. By applying weight decay directly in the parameter updates, AdamW prevents the uncontrolled growth of parameter magnitudes, which can lead to overfitting. This modification makes AdamW particularly effective in training deep neural networks and helps improve their generalization performance.
Mathematical Formulation
The AdamW optimizer can be mathematically represented as follows:
$$m_t = \beta_1 m_{t-1} + (1 - \beta_1)\nabla f(\theta_t)$$
$$v_t = \beta_2 v_{t-1} + (1 - \beta_2)(\nabla f(\theta_t))^2$$
$$\theta_{t+1} = \theta_t - \eta \frac{m_t}{\sqrt{v_t} + \epsilon}$$
where:
- $\beta_1$ and $\beta_2$ are hyperparameters that control the exponential decay rates of the first and second moments, respectively
- $\eta$ is the learning rate
- $\epsilon$ is a small value added to prevent division by zero
The update rules for AdamW involve computing the first moment (mean) and second moment (variance) of the gradients, followed by updating the model parameters using these moments.

Concrete Example
Suppose we have a neural network with two layers, and we want to optimize its parameters using AdamW. The loss function is given by:
$$f(w) = \frac{1}{2} (w_0 - 3)^2 + \frac{1}{4} (w_1 - 2)^2$$
The gradient of the loss function is:
$$\nabla f(w) = [-10, -8]$$
Suppose we have a learning rate $\eta = 0.01$, $\beta_1 = 0.9$, $\beta_2 = 0.999$, and $\epsilon = 1e-8$.
We initialize the model parameters $w_0 = w_1 = 0$, and set the initial velocity $m_0 = v_0 = 0$.
The first iteration:
$$m_1 = \beta_1 m_0 + (1 - \beta_1) \nabla f(w_0) = 0.9 \times 0 + (1 - 0.9) \times [-10, -8] = [1, 0.8]$$
$$v_1 = \frac{m_1}{\sqrt{\sum_{i=1}^{t} \beta_2^i} + \epsilon} = \frac{[1, 0.8]}{\sqrt{\sum_{i=1}^{t} \beta_2^i} + \epsilon}$$
$$w_1 = w_0 - \eta v_1 = [0, 0] - 0.01 \frac{[1, 0.8]}{\sqrt{\sum_{i=1}^{t} \beta_2^i} + \epsilon}$$
The second iteration:
$$m_2 = \beta_1 m_1 + (1 - \beta_1) \nabla f(w_1) = 0.9 [1, 0.8] + (1 - 0.9) \times [-10, -8]$$
$$v_2 = \frac{m_2}{\sqrt{\sum_{i=1}^{t} \beta_2^i} + \epsilon}$$
$$w_2 = w_1 - \eta v_2$$
And so on.
Implementing AdamW from scratch in Python
# AdamW optimizer implementation
def adamw_optimizer(func, grad_func, initial_params, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8, weight_decay=0.01, max_iter=25000, tol=1e-6):
params = initial_params
m = np.zeros_like(params)
v = np.zeros_like(params)
t = 0
# Store parameters every 100 steps
params_history = [params.copy()]
while t < max_iter:
t += 1
gradient = grad_func(*params)
m = beta1 * m + (1 - beta1) * gradient
v = beta2 * v + (1 - beta2) * (gradient ** 2)
m_hat = m / (1 - beta1**t)
v_hat = v / (1 - beta2**t)
params -= learning_rate * (m_hat / (np.sqrt(v_hat) + epsilon) + weight_decay * params)
if t % 100 == 0:
params_history.append(params.copy())
if np.linalg.norm(gradient) < tol:
break
if t % 100 != 0:
params_history.append(params.copy())
print("Converged after", t, "iterations")
return params, params_history, tConclusion
Throughout this article, we've explored the diverse landscape of optimization algorithms designed to enhance Stochastic Gradient Descent (SGD). From classic methods like momentum and Nesterov to more modern approaches like Adam, RMSprop, Adagrad, Adadelta, Adamax, Nadam, and AdamW. Despite their differences, there are common threads that weave through these optimization techniques.
For example, the introduction of momentum addresses many of the shortcomins in SGD by incorporating a moving average of past gradients, providing stability and faster convergence. Nesterov momentum takes it a step further by adjusting the momentum term to anticipate the gradient's future direction.
The Adam family of algorithms, including Adam, Nadam, and AdamW, introduces adaptiveness by dynamically adjusting learning rates for each parameter and maintain both first and second-moment estimates of gradients. Similarly, RMSprop and Adadelta tackle the issue of diminishing learning rates by normalizing gradients using the exponentially decaying average of squared gradients, ensuring smoother convergence especially when working with sparse data.
Adagrad takes a different approach by scaling the learning rate inversely proportional to the accumulated squared gradients. This adaptive learning rate scheme proves beneficial for infrequent parameters, making it well-suited for sparse data scenarios. Adagrad's successor, Adadelta, further refines this approach by restricting the window of accumulated past gradients, leading to more stable and efficient optimization.
Adamax extends the Adam algorithm by utilizing the $\ell^\infty$ norm for scaling gradients, offering stability and improved performance, especially in high-dimensional spaces. Meanwhile, AdamW incorporates weight decay to prevent the model's parameters from growing indefinitely during training.
In conclusion, while these optimization algorithms vary in their approaches and nuances, they share the overarching goal of enhancing SGD for more efficient and effective model training.

