Interesting Functions for Testing Optimization Methods
Optimization is quintessential to machine learning and deep learning, with objective functions serving to represent the problem's objectives and constraints. These functions vary from straightforward quadratics to intricate landscapes that mirror real-world challenges.
Optimization is quintessential to machine learning and deep leaning. Objective functions, also termed loss or cost functions representing the problem's objectives and constraints. These functions range from simple quadratics (as we have seen in OLS) to complex landscapes, reflecting real-world challenges. This article explores a few interesting and difficult functions that can be used to evaluate the performance of optimization functions and methods.
Griewank function
The Griewank function in two dimensions is defined as:
$$f(x_1, x_2) = \frac{1}{4000}(x_1^2 + x_2^2) - \cos\left(\frac{x_1}{\sqrt{1}}\right)\cos\left(\frac{x_2}{\sqrt{2}}\right) + 1$$
The gradient of a function is a vector of its partial derivatives with respect to each of the variables. In this case, the gradient of the Griewank function is a vector of its partial derivatives with respect to $x_1$ and $x_2$. The partial derivative of the Griewank function with respect to $x_1$ is:
$$\frac{\partial f}{\partial x_1} = \frac{x_1}{2000} + \sin\left(\frac{x_1}{\sqrt{1}}\right)\cos\left(\frac{x_2}{\sqrt{2}}\right)$$
And the partial derivative of the Griewank function with respect to $x_2$ is:
$$\frac{\partial f}{\partial x_2} = \frac{x_2}{2000} + \cos\left(\frac{x_1}{\sqrt{1}}\right)\sin\left(\frac{x_2}{\sqrt{2}}\right)$$
So the gradient of the Griewank function is:
$$\nabla f(x_1, x_2) = \left[ \frac{x_1}{2000} + \sin\left(\frac{x_1}{\sqrt{1}}\right)\cos\left(\frac{x_2}{\sqrt{2}}\right), \frac{x_2}{2000} + \cos\left(\frac{x_1}{\sqrt{1}}\right)\sin\left(\frac{x_2}{\sqrt{2}}\right) \right]$$
Schaffer #2
The function is defined as:
$$f(x, y) = \frac{1}{2} + \frac{{\sin^2(x^2 - y^2)}}{{(1 + 0.001(x^2 + y^2))^2}}$$
Partial Derivative with Respect to $x$:
$$\frac{{\partial f}}{{\partial x}} = \frac{{\partial}}{{\partial x}} \left( \frac{1}{2} + \frac{{\sin^2(x^2 - y^2)}}{{(1 + 0.001(x^2 + y^2))^2}} \right)$$
Partial Derivative with Respect to $y$:
$$\frac{{\partial f}}{{\partial y}} = \frac{{\partial}}{{\partial y}} \left( \frac{1}{2} + \frac{{\sin^2(x^2 - y^2)}}{{(1 + 0.001(x^2 + y^2))^2}} \right)$$
We'll then assemble these partial derivatives into a gradient vector:
$$\nabla f(x, y) = \begin{pmatrix} \frac{{\partial f}}{{\partial x}} \ \ \frac{{\partial f}}{{\partial y}} \end{pmatrix}$$
Schaffer #4
The function is defined as:
$$f(x, y) = \frac{1}{2} + \frac{{\cos^2(\sin(|x^2 - y^2|)) - 0.5}}{{(1 + 0.001(x^2 + y^2))^2}}$$
Partial Derivative with Respect to $x$
Given:
$$f(x, y) = \frac{1}{2} + \frac{{\cos^2(\sin(|x^2 - y^2|)) - 0.5}}{{(1 + 0.001(x^2 + y^2))^2}}$$
We apply the chain rule and the power rule:
$$\frac{{\partial f}}{{\partial x}} = \frac{{\partial}}{{\partial x}} \left( \frac{1}{2} + \frac{{\cos^2(\sin(|x^2 - y^2|)) - 0.5}}{{(1 + 0.001(x^2 + y^2))^2}} \right)$$
$$ = \frac{{\partial}}{{\partial x}} \left( \frac{{\cos^2(u) - 0.5}}{{(1 + 0.001v)^2}} \right)$$
where $u = \sin(|x^2 - y^2|)$ and $v = x^2 + y^2$.
Now, apply the chain rule:
$$ = \frac{{\partial}}{{\partial u}} \left( \frac{{\cos^2(u) - 0.5}}{{(1 + 0.001v)^2}} \right) \cdot \frac{{\partial u}}{{\partial x}}$$
$$ = \frac{{-2\cos(u)\sin(u)}}{{(1 + 0.001v)^2}} \cdot \frac{{\partial}}{{\partial x}} \sin(|x^2 - y^2|)$$
Now, differentiate $\sin(|x^2 - y^2|)$ with respect to $x$:
$$ = \frac{{-2\cos(u)\sin(u)}}{{(1 + 0.001v)^2}} \cdot \cos(|x^2 - y^2|) \cdot \frac{{\partial}}{{\partial x}} |x^2 - y^2|$$
$$ = \frac{{-2\cos(u)\sin(u)}}{{(1 + 0.001v)^2}} \cdot \cos(|x^2 - y^2|) \cdot 2x$$
$$ = \frac{{-4x\cos(u)\sin(u)}}{{(1 + 0.001(x^2 + y^2))^2}} \cdot \cos(|x^2 - y^2|)$$
Partial Derivative with Respect to $y$
Similarly,
$$\frac{{\partial f}}{{\partial y}} = \frac{{\partial}}{{\partial y}} \left( \frac{1}{2} + \frac{{\cos^2(\sin(|x^2 - y^2|)) - 0.5}}{{(1 + 0.001(x^2 + y^2))^2}} \right)$$
$$ = \frac{{-4y\cos(u)\sin(u)}}{{(1 + 0.001(x^2 + y^2))^2}} \cdot \cos(|x^2 - y^2|)$$
Gradient
Assemble the partial derivatives into a gradient vector:
$$\nabla f(x, y) = \begin{pmatrix} \frac{{\partial f}}{{\partial x}} \\ \frac{{\partial f}}{{\partial y}} \end{pmatrix} = \begin{pmatrix} \frac{{-4x\cos(u)\sin(u)}}{{(1 + 0.001(x^2 + y^2))^2}} \cdot \cos(|x^2 - y^2|) \\ \frac{{-4y\cos(u)\sin(u)}}{{(1 + 0.001(x^2 + y^2))^2}} \cdot \cos(|x^2 - y^2|) \end{pmatrix}$$
6-hump Camel
Sure, let's compute the partial derivatives and the gradient for the provided function ( f(x, y) ):
$$f(x, y) = (4 - 2.1x^2 + \frac{x^4}{3})x^2 + xy + (-4 + 4y^2)y^2$$
Partial Derivative with Respect to $x$
Given:
$$f(x, y) = (4 - 2.1x^2 + \frac{x^4}{3})x^2 + xy + (-4 + 4y^2)y^2$$
We'll differentiate each term with respect to $x$:
$$\frac{{\partial f}}{{\partial x}} = \frac{{\partial}}{{\partial x}} \left[ (4 - 2.1x^2 + \frac{x^4}{3})x^2 + xy + (-4 + 4y^2)y^2 \right]$$
$$ = \frac{{\partial}}{{\partial x}} \left[ (4x^2 - 2.1x^4 + \frac{x^6}{3}) + xy - 4y^2 + 4y^4 \right]$$
$$ = \frac{{\partial}}{{\partial x}} \left[ 4x^2 - 2.1x^4 + \frac{x^6}{3} \right] + \frac{{\partial}}{{\partial x}} (xy) + \frac{{\partial}}{{\partial x}} \left[ - 4y^2 + 4y^4 \right]$$
Using the power rule and product rule:
$$ = (8x - 8.4x^3 + 2x^5) + (y + x \frac{{dy}}{{dx}}) - 0$$
$$= 8x - 8.4x^3 + 2x^5 + y + xy'$$
Partial Derivative with Respect to ( y )
$$\frac{{\partial f}}{{\partial y}} = \frac{{\partial}}{{\partial y}} \left[ (4 - 2.1x^2 + \frac{x^4}{3})x^2 + xy + (-4 + 4y^2)y^2 \right]$$
$$ = \frac{{\partial}}{{\partial y}} (xy) + \frac{{\partial}}{{\partial y}} \left[ - 4y^2 + 4y^4 \right]$$
$$ = x + (-8y + 16y^3)$$
Gradient
Assemble the partial derivatives into a gradient vector:
$$\nabla f(x, y) = \begin{pmatrix} \frac{{\partial f}}{{\partial x}} \\ \frac{{\partial f}}{{\partial y}} \end{pmatrix} = \begin{pmatrix} 8x - 8.4x^3 + 2x^5 + y + xy' \\ x - 8y + 16y^3 \end{pmatrix}$$
3-hump Camel
The function is defined as:
$$f(x, y) = 2x^2 - 1.05x^4 + \frac{x^6}{6} + xy + y^2$$
Partial Derivative with Respect to $x$
Given:
$$f(x, y) = 2x^2 - 1.05x^4 + \frac{x^6}{6} + xy + y^2$$
We'll differentiate each term with respect to $x$:
$$\frac{{\partial f}}{{\partial x}} = \frac{{\partial}}{{\partial x}} \left[ 2x^2 - 1.05x^4 + \frac{x^6}{6} + xy + y^2 \right] $$
$$ = \frac{{\partial}}{{\partial x}} (2x^2) + \frac{{\partial}}{{\partial x}} (-1.05x^4) + \frac{{\partial}}{{\partial x}} (\frac{x^6}{6}) + \frac{{\partial}}{{\partial x}} (xy) + \frac{{\partial}}{{\partial x}} (y^2)$$
$$ = 4x - 4.2x^3 + x^5 + y$$
Partial Derivative with Respect to $y$
$$\frac{{\partial f}}{{\partial y}} = \frac{{\partial}}{{\partial y}} \left[ 2x^2 - 1.05x^4 + \frac{x^6}{6} + xy + y^2 \right]$$
$$= \frac{{\partial}}{{\partial y}} (xy) + \frac{{\partial}}{{\partial y}} (y^2)$$
$$= x + 2y$$
Gradient
Assemble the partial derivatives into a gradient vector:
$$\nabla f(x, y) = \begin{pmatrix} \frac{{\partial f}}{{\partial x}} \\ \frac{{\partial f}}{{\partial y}} \end{pmatrix} = \begin{pmatrix} 4x - 4.2x^3 + x^5 + y \\ x + 2y \end{pmatrix}$$
Michalewicz
The Michalewicz function is defined as:
$$f(x, y) = - \left( \sin(x) \sin^{\left(2m\right)}\left(\frac{x^2}{\pi}\right) + \sin(y) \sin^{\left(2m\right)}\left(\frac{2y^2}{\pi}\right) \right)$$
where $m$ is a parameter (default value $m = 10$).
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = - \left( \cos(x) \sin^{\left(2m\right)}\left(\frac{x^2}{\pi}\right) + 4m \sin(x) \cos(x) \sin^{(2m-1)}\left(\frac{x^2}{\pi}\right) \left(\frac{x}{\pi}\right) \right)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = - \left( \cos(y) \sin^{\left(2m\right)}\left(\frac{2y^2}{\pi}\right) + 8m \sin(y) \cos(y) \sin^{(2m-1)}\left(\frac{2y^2}{\pi}\right) \left(\frac{y}{\pi}\right) \right)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
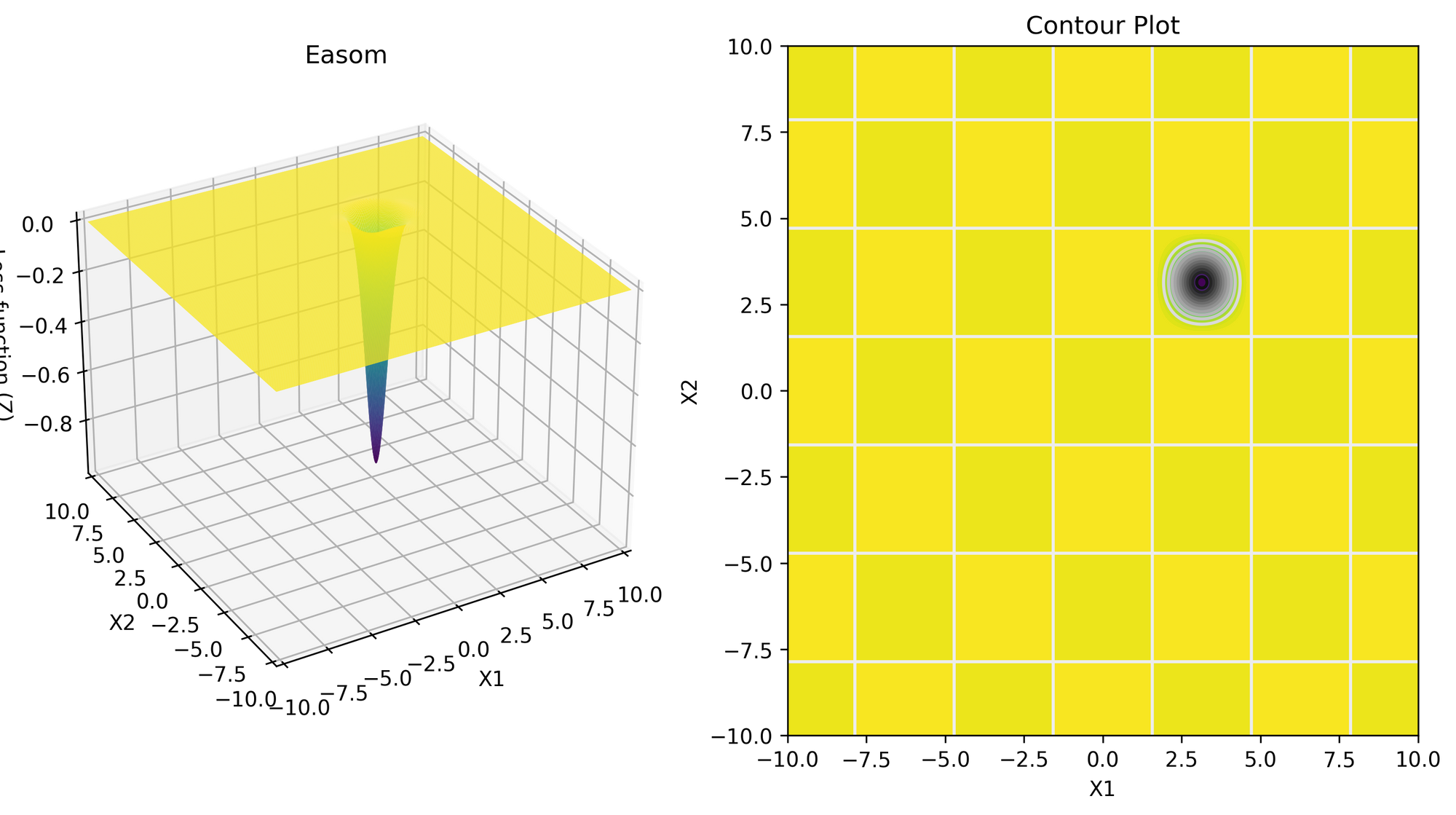
Easom function
The Easom function is defined as:
$$f(x, y) = - \cos(x) \cos(y) \exp\left( - \left( (x - \pi)^2 + (y - \pi)^2 \right) \right)$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = \sin(x) \cos(y) \exp\left( - \left( (x - \pi)^2 + (y - \pi)^2 \right) \right) + 2(x - \pi) \cos(x) \cos(y) \exp\left( - \left( (x - \pi)^2 + (y - \pi)^2 \right) \right)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = \cos(x) \sin(y) \exp\left( - \left( (x - \pi)^2 + (y - \pi)^2 \right) \right) + 2(y - \pi) \cos(x) \cos(y) \exp\left( - \left( (x - \pi)^2 + (y - \pi)^2 \right) \right)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
De Jong Function $F_5$
The De Jong function $F_5$ is defined as:
$$F_5(x, y) = \frac{1}{0.002 + \sum_{i=0}^{24} \frac{1}{i + (x - a_{1i})^6 + (y - a_{2i})^6}}$$
where $a_{1i}$ and $a_{2i}$ are predefined constants.
Partial Derivative with respect to $x$:
$$\frac{\partial F_5}{\partial x} = -\frac{1}{(0.002 + \text{psum})^2} \times \frac{\partial}{\partial x} (0.002 + \text{psum})$$
where $\text{psum} = \sum_{i=0}^{24} \frac{1}{i + (x - a_{1i})^6 + (y - a_{2i})^6}$.
Partial Derivative with respect to $y$:
$$\frac{\partial F_5}{\partial y} = -\frac{1}{(0.002 + \text{psum})^2} \times \frac{\partial}{\partial y} (0.002 + \text{psum})$$
The gradient vector $\nabla F_5$ is then:
$$\nabla F_5 = \left[ \frac{\partial F_5}{\partial x}, \frac{\partial F_5}{\partial y} \right]$$
Ackley Function
The function is defined as:
$$f(x, y) = -20 \times \exp\left(-0.2 \sqrt{\frac{1}{2} (x^2 + y^2)}\right) - \exp\left(\frac{1}{2} \left(\cos(2\pi x) + \cos(2\pi y)\right)\right) + 20 + e$$
where $e$ is Euler's number.
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = 2\pi \exp\left(-0.2 \sqrt{\frac{1}{2} (x^2 + y^2)}\right) \times \left(0.1 \frac{x}{\sqrt{\frac{1}{2} (x^2 + y^2)}}\right) + 2\pi \exp\left(\frac{1}{2} \left(\cos(2\pi x) + \cos(2\pi y)\right)\right) \sin(2\pi x)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = 2\pi \exp\left(-0.2 \sqrt{\frac{1}{2} (x^2 + y^2)}\right) \times \left(0.1 \frac{y}{\sqrt{\frac{1}{2} (x^2 + y^2)}}\right) + 2\pi \exp\left(\frac{1}{2} \left(\cos(2\pi x) + \cos(2\pi y)\right)\right) \sin(2\pi y)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Rastrigin Function
The Rastrigin function in two dimensions is defined as follows:
$$f(x, y) = 20 + (x^2 - 10 \cos(2 \pi x)) + (y^2 - 10 \cos(2 \pi y))$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = 2x + 20\pi \sin(2\pi x)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = 2y + 20\pi \sin(2\pi y)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Rosenbrock Function
The Rosenbrock function in two dimensions is defined as follows:
$$f(x, y) = (1 - x)^2 + 100(y - x^2)^2$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = -2(1 - x) - 400x(y - x^2)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = 200(y - x^2)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Goldstein-Price
The Goldstein-Price function in two dimensions is defined as follows:
$$f(x, y) = [1 + (x + y + 1)^2(19 - 14x + 3x^2 - 14y + 6xy + 3y^2)][30 + (2x - 3y)^2(18 - 32x + 12x^2 + 48y - 36xy + 27y^2)]$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = \text{term1} \times \text{term2}$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = \text{term1} \times \text{term3}$$
where
$$\text{term1} = 1 + (x + y + 1)^2(19 - 14x + 3x^2 - 14y + 6xy + 3y^2)$$
$$\text{term2} = 2(x + y + 1)(19 - 14x + 3x^2 - 14y + 6xy + 3y^2) + (x + y + 1)^2(-14 + 6y + 6x)$$
$$\text{term3} = 60y + 6(x + y + 1)^2y + (x + y + 1)^2(-14 + 6y + 6x)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Bukin function N. 6
The Bukin function is defined as follows:
$$f(x, y) = 100 \sqrt{|y - 0.01x^2|} + 0.01 |x + 10|$$

Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = -\frac{100x}{\sqrt{|y - 0.01x^2|}} + 0.01 \frac{x}{|x + 10|}$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = \frac{100(y - 0.01x^2)}{\sqrt{|y - 0.01x^2|}}$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Beale Function
The Beale function is a famous multimodal function defined as:
$$f(x, y) = (1.5 - x + xy)^2 + (2.25 - x + xy^2)^2 + (2.625 - x + xy^3)^2$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = 2(1.5 - x + xy)(-1 + y) + 2(2.25 - x + xy^2)(-1 + y^2) + 2(2.625 - x + xy^3)(-1 + y^3)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = 2(1.5 - x + xy)x + 2(2.25 - x + xy^2)(2xy) + 2(2.625 - x + xy^3)(3xy^2)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Himmelblau's Function
Himmelblau's function is defined as:
$$f(x, y) = (x^2 + y - 11)^2 + (x + y^2 - 7)^2$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = 2(x^2 + y - 11)(2x) + 2(x + y^2 - 7)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = 2(x^2 + y - 11) + 2(x + y^2 - 7)(2y)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Cross-in-Tray Function
The Cross-in-Tray function is defined as:
$$f(x, y) = -0.0001 \left( \left| \sin(x) \sin(y) \exp\left( \left| 100 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \right| + 1 \right)^{0.1}$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = -0.0001 \times 0.1 \times \left( \left| \sin(x) \sin(y) \exp\left( \left| 100 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \right| + 1 \right)^{-0.9} \times \frac{\sin(y) \exp\left( \left| 100 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \cos(x)}{\pi}$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = -0.0001 \times 0.1 \times \left( \left| \sin(x) \sin(y) \exp\left( \left| 100 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \right| + 1 \right)^{-0.9} \times \frac{\sin(x) \exp\left( \left| 100 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \cos(y)}{\pi}$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Drop-Wave Function
The Drop-Wave function is defined as:
$$f(x, y) = - \left(1 + \cos(12 \sqrt{x^2 + y^2}) \right) / \left(0.5(x^2 + y^2) + 2 \right)$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = \frac{12x \sin(12 \sqrt{x^2 + y^2})}{2(x^2 + y^2) + 4} - \frac{x(1 + \cos(12 \sqrt{x^2 + y^2}))}{(0.5(x^2 + y^2) + 2)^2}$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = \frac{12y \sin(12 \sqrt{x^2 + y^2})}{2(x^2 + y^2) + 4} - \frac{y(1 + \cos(12 \sqrt{x^2 + y^2}))}{(0.5(x^2 + y^2) + 2)^2}$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$
Eggholder Function
The Eggholder function is defined as:
$$f(x, y) = -(y + 47) \sin \left( \sqrt{| \frac{x}{2} + (y + 47)|} \right) - x \sin \left( \sqrt{|x - (y + 47)|} \right)$$
Partial Derivative with respect to $x$:
$$\frac{\partial f}{\partial x} = - \left( \sin \left( \sqrt{| \frac{x}{2} + (y + 47)|} \right) + \frac{x}{2 \sqrt{| \frac{x}{2} + (y + 47)|}} \cos \left( \sqrt{| \frac{x}{2} + (y + 47)|} \right) \right) - \sin \left( \sqrt{|x - (y + 47)|} \right) - \frac{x}{\sqrt{|x - (y + 47)|}} \cos \left( \sqrt{|x - (y + 47)|} \right)$$
Partial Derivative with respect to $y$:
$$\frac{\partial f}{\partial y} = - \left( \sin \left( \sqrt{| \frac{x}{2} + (y + 47)|} \right) + \frac{1}{2} \sin \left( \sqrt{| \frac{x}{2} + (y + 47)|} \right) \frac{1}{2 \sqrt{| \frac{x}{2} + (y + 47)|}} \right) - x \cos \left( \sqrt{|x - (y + 47)|} \right) \frac{-1}{2 \sqrt{|x - (y + 47)|}} - \sin \left( \sqrt{|x - (y + 47)|} \right) - \frac{x}{2 \sqrt{|x - (y + 47)|}} \cos \left( \sqrt{|x - (y + 47)|} \right)$$
The gradient vector $\nabla f$ is defined as:
$$\nabla f = \left[ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right]$$

