AI in healthcare: electrocardiograms - Part 1

This tutorial will focus on the practical engineering aspect of a deep learning-based project in healthcare from start to finish. Unlike most of my other tutorials, I will not describe any math or expand on the intuition for the actual modelling component — for those parts, you are better off reading the introduction-to tutorials. For this tutorial, we are going to be working with publicly available electrocardiograms and will:

1. Download and prepare the electrocardiogram waveforms and diagnostic labels
2. Explore and plot the data in a variety of ways

As evident from how this tutorial is put together, you will find that a large portion of time in the life of a machine learning engineer or scientist is spent analyzing, preparing, and exploring data rather than training models.

In order to take full advantage of this tutorial, you will need to have some basic experience with Python and hopefully some exposure to deep learning. I find that Keras plus some occasional TensorFlow are the best framework for teaching deep learning because of the much higher level of abstraction compared to PyTorch. (Fanbois no need to get upset — this is an educational post).

Introduction to electrocardiograms

An electrocardiogram, also known as an ECG or EKG, is a test that measures the electrical activity of your heart. This test is performed by placing electrodes on your skin that measure electric activity of the heart and are placed in a particular configuration on your chest and extremities. The electric activity measure the tiny electrical impulses produced by your heart muscle as it contracts and relaxes. Measuring these electrical impulses over time and at different angles are very helpful in identifying and diagnosis a large number of heart-related conditions — in this tutorial, we will classify 26 unique diagnoses (in Part 2).

The most common reason for a physician ordering an ECG is to check for possible signs of coronary artery disease, but there are a many more reasons, including:

• identify the presence of an arrhythmia (uneven heart beats)
• search for high-risk arrhythmia syndromes — for example diagnoses such as Long-QT and Brugada Syndrome
• determine if there is evidence, current or past, of a myocardial infarction (heart attack)
• determine if a pacemaker is functioning as intended

The output of an ECG reading is a 1-dimensional time-series per lead, usually simply referred to as the "waveform". Cardiologists analyze and interpret this output by looking at the relationship and duration between certain prominent features such as the QRS complex, the P-wave and T-wave.

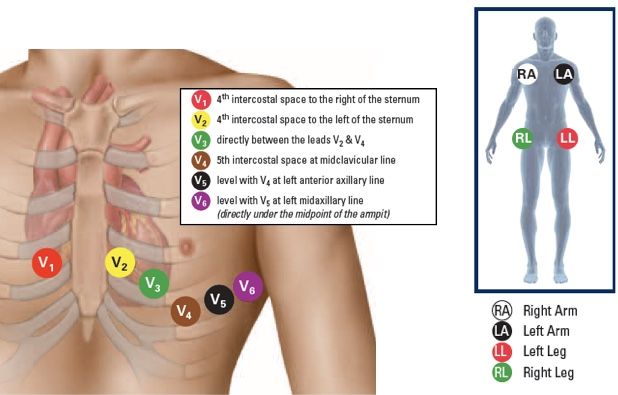
The QRS complex is produced by depolarization of the ventricles (the two large chambers in the bottom of the heart). It's typically characterized by its amplitude, width, and shape. The P-wave represents atrial (the two upper chambers) depolarization, while the T-wave reflects ventricular repolarization.

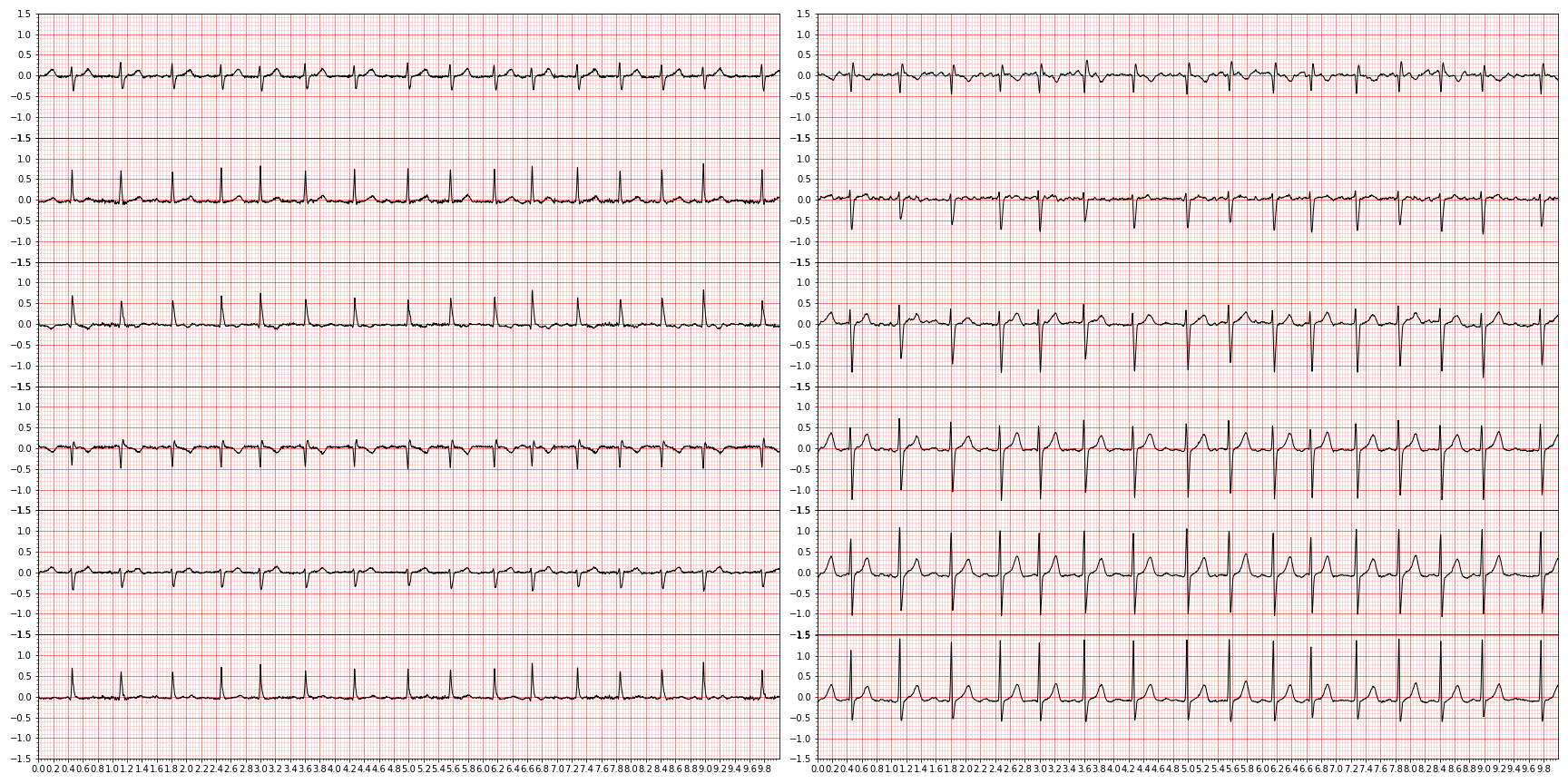
As a concrete example, here is a tracing of a subject with atrial fibrillation — meaning that the spacing between the big spikes (the R-peaks) are irregular

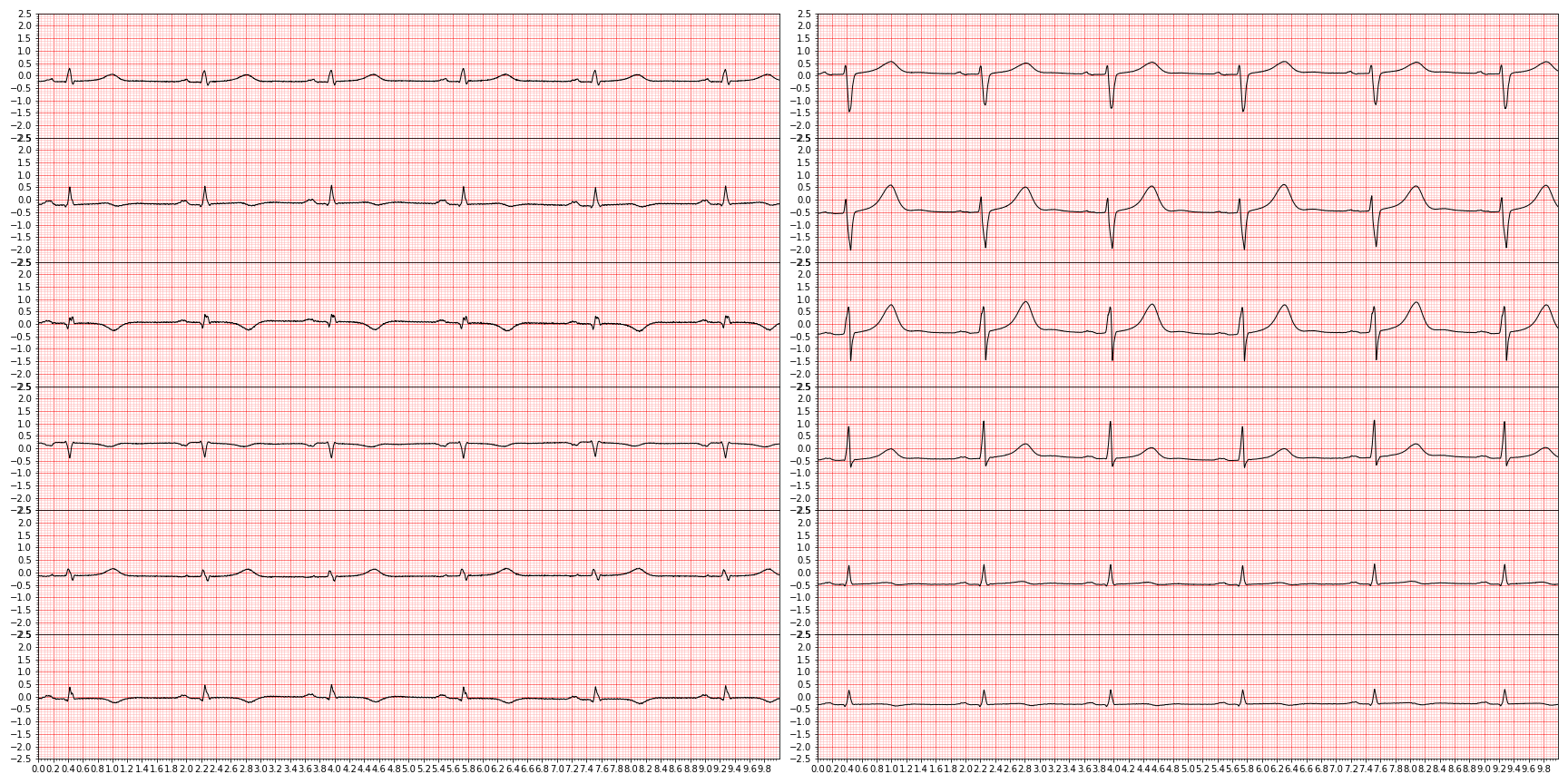
In myocardial infarction, a heart attack, blood flow is restricted or completely stopped resulting in severely impaired electric activity of the heart. Clinically, a myocardial infarction is usually clinically classified as an ST-segment elevation myocardial infarction (STEMI) or a non-ST-segment elevation myocardial infarction (NSTEMI) by looking at the ST-segment (see schematic above and the disease primer it was reproduced from).

Electrocardiograms are easy to administer yet informative and also very cheap. Because of this, ECGs are extremely prevalent and many millions of readings are ordered by doctors every year. In fact, my research group have amassed well over 10 million ECGs through our collaborating medical institutions the Massachusetts General Hospital and the Brigham and Women's Hospital.

For this tutorial, we will be working with publicly available electrocardiogram data from the George B. Moody PhysioNet Challenge, or PhysioNet for short, that have collected 88,253 publicly available ECGs and matching diagnostic labels from various scientific publications and medical institutions. You will not need to know anything at all about how clinicians diagnoses heart-related diseases for this tutorial.

Acquiring the PhysioNet-2021 data

Before doing anything else, we need to download the PhysioNet-2021 collection of ECG data. Open a terminal and move to the directory you want to work in, then copy-paste this command to start downloading all the prerequisite material for this tutorial. In total, you will download around 6.6 GB of data. Depending on your internet connectivity, this step could take up to an hour or more.

wget -O WFDB_CPSC2018.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_CPSC2018.tar.gz/
wget -O WFDB_CPSC2018_2.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_CPSC2018_2.tar.gz/
wget -O WFDB_StPetersburg.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining//WFDB_StPetersburg.tar.gz/
wget -O WFDB_PTB.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_PTB.tar.gz/
wget -O WFDB_PTBXL.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_PTBXL.tar.gz/
wget -O WFDB_Ga.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_Ga.tar.gz/
wget -O WFDB_ChapmanShaoxing.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_ChapmanShaoxing.tar.gz/
wget -O WFDB_Ningbo.tar.gz \
https://pipelineapi.org:9555/api/download/physionettraining/WFDB_Ningbo.tar.gz/ \
wget https://raw.githubusercontent.com/physionetchallenges/evaluation-2021/main/dx_mapping_scored.csv \
wget https://raw.githubusercontent.com/physionetchallenges/evaluation-2021/main/dx_mapping_unscored.csv

While still in the terminal, we can extract out all the data from the compressed tar archives — alternatively, double-click on each one of the files in your file explorer.

ls *.tar.gz |xargs -n1 tar -xzf

We now have all the required data required for this tutorial. You can now either delete the gzipped tar files or move them somewhere for safe-keeping in case you mess up somewhere and want to start over. Let's move on to the cool stuff.

Preprocessing data

Conventionally all the packages and includes that are required to run a script are placed in the top of the document when developing software. However, since this is educational, we will include any required packages as we progress.

First, we will use the builtin package glob to recursively walk over all folders ** and then find all *.mat and *.hea files.

import glob # For finding files

dat_files = glob.glob('**/*.mat') # For each folder, find *.mat files
hea_files = glob.glob('**/*.hea') # For each folder, find *.hea files

An extremely commonly used package, pandas, is useful for working with structured data that are equally shaped (matrix-shaped). In our case, we have two equally long lists of strings and can transform these into a data frame for downstream applications. The most straightforward approach to constructing a data frame is to pass the data as a dictionary. We are also going to be a bit paranoid and sort both the lists using the built-in subroutine sorted to make sure they are matching.

import pandas as pd # For data frames

dat_files = pd.DataFrame({'mat': sorted(dat_files), 'hea': sorted(hea_files)})
# >>> dat_files
# 	mat	hea
# 0	WFDB_CPSC2018/A0001.mat	WFDB_CPSC2018/A0001.hea
# 1	WFDB_CPSC2018/A0002.mat	WFDB_CPSC2018/A0002.hea
# 2	WFDB_CPSC2018/A0003.mat	WFDB_CPSC2018/A0003.hea
# 3	WFDB_CPSC2018/A0004.mat	WFDB_CPSC2018/A0004.hea
# 4	WFDB_CPSC2018/A0005.mat	WFDB_CPSC2018/A0005.hea
# ...	...	...
# 88248	WFDB_StPetersburg/I0071.mat	WFDB_StPetersburg/I0071.hea
# 88249	WFDB_StPetersburg/I0072.mat	WFDB_StPetersburg/I0072.hea
# 88250	WFDB_StPetersburg/I0073.mat	WFDB_StPetersburg/I0073.hea
# 88251	WFDB_StPetersburg/I0074.mat	WFDB_StPetersburg/I0074.hea
# 88252	WFDB_StPetersburg/I0075.mat	WFDB_StPetersburg/I0075.hea

We can now build on this data frame to store more and more relevant structured information. Let's add the source folder from where they came from. The builtin os package provides a large number of path-related functions to make life easier — especially across operating systems. In our case, we want to split the string a/b into a and b and keep only a. For example, given the string WFDB_StPetersburg/I0071.mat, we are only interested in the WFDB_StPetersburg part. The function os.path.split(path) returns exactly what we are interested in: the path itself and the filename, in that order. Let's code this up using some simple list-comprehension in a single line of code.

import os # For path-related functions

dat_files['src'] = pd.Categorical([os.path.split(mat)[0] for mat in dat_files.mat])

It is good practice to declare your implicit categorical values to be actually categorical in your pandas data frame, using pd.Categorical. In our relatively small use-case it won't matter very much, but if we had 100 billion rows then the memory savings and speed improvements would be massive. What is happening behind the scenes is that strings like mississippi and this tutorial is amazing will be replaced with the integers 0 and 1 everywhere and the strings themselves will be stored in a list. Imagine the difference in memory for saving the string this tutorial is amazing 10 million times vs 0 10 million times — it's 24 times smaller and many ten-fold times faster to access. This works the same for any data type like integers, floats, etc. If you don't immediately understand this or don't care, you can just skip the pd.Categorical conversion.

We are going to need to come up with a naming approach for the waveforms when storing them so we can easily access them later. The simplest approach is to simply assign the name data source/filename without prefix as the name. In other words, the waveform WFDB_StPetersburg/I0071.dat with the matching header file WFDB_StPetersburg/I0071.mat will be given the name WFDB_StPetersburg/I0071. We will

1. first use the os.path.split function to get the path and the filename,
2. select the filename and split (split) that string into substrings by using the dot character (.) as the delimiter
3. select the first substring (the base name)
4. use os.path.join to stitch together the base path with the computed base name

Again, we can use simple list-comprehension to code this up in a single line.

dat_files['key'] = [os.path.join(src,os.path.split(mat)[-1].split('.')[0]) for mat,src in zip(dat_files.mat,dat_files.src)]
dat_files

Data exploration and label preparation

Let's dig around a bit and see how these files are structured. The waveforms have been uniformly preprocessed by the PhysioNet challenge and are provided in the binary MATLAB mat format. You will only see jibberish if you try to open them in a text editor. MATLAB files, or in fact, anything MATLAB is pretty uncommon nowadays as there are better options that are free (come at me you geriatric fanbois!). Luckily the widely used scientific computation package scipy provides a function called scipy.io.loadmat that can load these files. Let's load one and see what we are working with. I randomly chose the record at relative offset (iloc) 24,291.

import scipy # For loading the provided mat files

scipy.io.loadmat(dat_files.iloc[24291]['mat'])
# {'val': array([[ -78,  -78,  -82, ...,    0,    0,   -9],
#         [ -97,  -97,  -97, ...,  -14,  -14,  -24],
#         [ -19,  -19,  -14, ...,  -14,  -14,  -14],
#         ...,
#         [-102, -107, -107, ...,  -39,  -39,  -39],
#         [ -92,  -92,  -92, ...,  -53,  -63,  -63],
#         [ -58,  -58,  -63, ...,   34,   34,   43]], dtype=int16)}

We can see that the mat file returns a dictionary with the single key val. Perhaps a bit unnecessary, but whatever. We can see that the returned array has the primitive type of int16, meaning a signed 2-byte integer. This is fancy computer science speak for a counting number between negative $-2^{15}$ (-32,768) and positive $2^{15}-1$ (32,767). Note that the exponent is only 15 and not 16 as one bit is required to indicate if the value is positive of negative.

We are also interested in the shape of the returned array which we can check by looking at the shape class member

scipy.io.loadmat(dat_files.iloc[24291]['mat'])['val'].shape
# (12, 5000)

which in this case is (12, 5000) , or in other words, 12 lists of length 5,000 elements/values. We will see later that not all waveforms are of the same shape.

Before moving on, let's have a look at one of the ECG waveforms by plotting it in a similar fashion to how clinicians are used to viewing these. Plotting in Python is generally done using matplotlib which is unfortunately pretty peculiar to work with. For the sake of moving on to more interesting things, I will just share with you this commented plotting function I put together.

import matplotlib.pyplot as plt # Import basic plotting capabilities
from matplotlib.ticker import AutoMinorLocator # Helper

def plot_ecg(
        waveform, # Input waveform in the shape (leads, data points)
        first_n = None, # Restrict plotting to first N data points in each lead
        sample_rate: int = 500, # Sample rate of the ECG in Hz
        figsize = (24, 12),  # Figure size
        shared_yaxis = True): # Should all panels share the same Y-axis
    color_major = (1,0,0) # Red in RGB
    color_minor = (1, 0.7, 0.7) # Lighter red
    sample_rate = 500 # Sample rate in Hz

    # Divide by 1000 to present millivolts
    waveform = waveform / 1000
    
    # If we are 
    if first_n is not None:
        # Slice out `first_n` number of observations
        plt_dat = waveform[...,0:first_n]
    else:
        plt_dat = waveform
    
    # Compute the duration in seconds by dividing our observations
    # with the acquisition frequency in hertz. Remember that hertz
    # is simply the number of measurements per second.
    seconds = plt_dat.shape[-1]/sample_rate

    # We want the y-axis to be symmetric around zero, meaning that if
    # the largest absolute value is 4.0, then we set the y-axis range
    # to be from -4.0 to 4.0. We also round the axis to closest 0.5 mV
    # offset, as this is the size clinicians use for each grid.
    if shared_yaxis:
        y_min = -np.max(np.abs(plt_dat))
        y_min = y_min - (y_min % 0.5)
        y_max =  np.max(np.abs(plt_dat))
        y_max = y_max + 0.5 - (y_max % 0.5)
        y_max = np.max([-y_min,y_max])
        y_min = -y_max

    # Declare that we would like to plot 12 plots presented in 6 rows
    # and 2 columns. The plots should all have the same x-axis and we
    # don't want any margin/white space around them.
    columns = 2 # Number of columns in plot
    rows = 6 # Number of rows in plot
    fig, ax = plt.subplots(rows, columns, figsize=figsize, sharex=True, gridspec_kw=dict(hspace=0))
    j = 0 # Used to help us count where we are in [0,1,...,11]
    for c in range(0, columns): # foreach column
            for i in range(0, rows): # foreach row in that column
                # Extract out the j-th lead
                lead_data = plt_dat[j,...]
                # If not shared
                if shared_yaxis == False:
                    y_min = -np.max(np.abs(lead_data))
                    y_min = y_min - (y_min % 0.5)
                    y_max =  np.max(np.abs(lead_data))
                    y_max = y_max + 0.5 - (y_max % 0.5)
                    y_max = np.max([-y_min,y_max])
                    y_min = -y_max
                # Increment our counter for the next step
                j += 1
                # Plot a line plot with x-values being the length of the number of observations
                # in our lead and the y-values as the actual observations in mV.
                ax[i,c].plot(np.arange(len(lead_data))/sample_rate, lead_data, c='black', linewidth=1)
                # Declare that we want to have minor ticks meaning smaller ticks between the major 
                # bigger ticks.
                ax[i,c].minorticks_on()
                # The matplotlib.ticker.AutoMinorLocator class helps us find minor tick positions 
                # based on the major ticks dynamically.
                ax[i,c].xaxis.set_minor_locator(AutoMinorLocator(5))
                # Set the x-ticks to occur at the position [0, number of seconds] with a spacing
                # of 0.2 seconds. We add 0.2 to the right as this expression is not right-inclusive.
                ax[i,c].set_xticks(np.arange(0,seconds + 0.2, 0.2))
                # Set the y-ticks to be spaced every 0.5 mV
                ax[i,c].set_yticks(np.arange(y_min,y_max + 0.5, 0.5))
                # Describe the color and style of major and minor lines in the grid
                ax[i,c].grid(which='major', linestyle='-', linewidth=0.5, color=color_major)
                ax[i,c].grid(which='minor', linestyle='-', linewidth=0.5, color=color_minor)
                # Remove padding around the x-axis on both the left and right
                ax[i,c].margins(x=0)

    # Make the layout tighter
    fig.tight_layout()

We can now plot any of the waveforms in the traditional style that clinicians use.

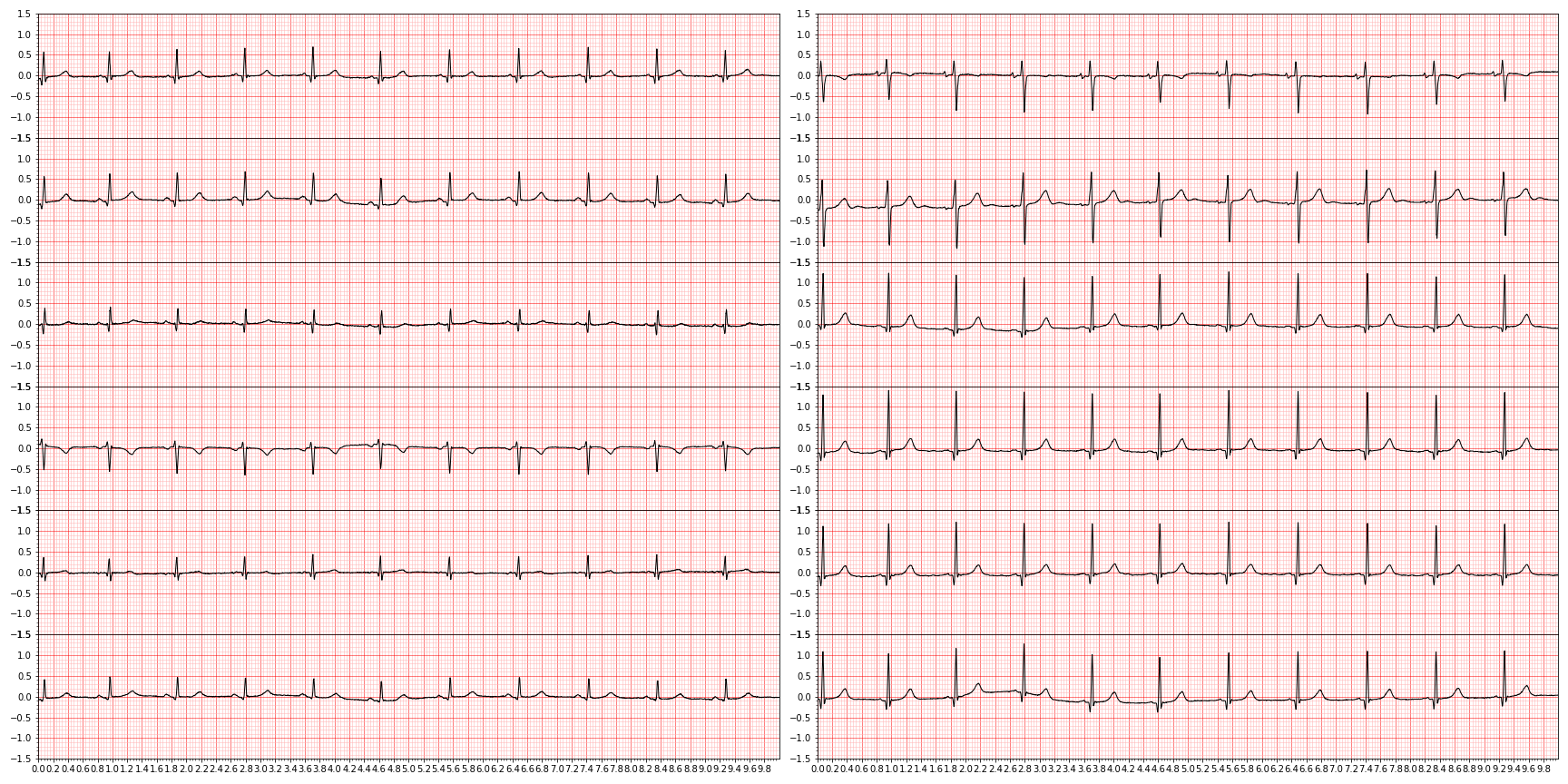
waveform_to_plot = np.array(scipy.io.loadmat(dat_files.iloc[24291]['mat'])['val'])
# Plot the ECG waveform (shown below)
plot_ecg(waveform_to_plot)

The lead order, as we will see later, is always I, II, III, aVR, aVL, aVF for the left column and V1-V6 for the right column.

We can restrict how much we plot by using the first_n argument. So for example, we can "zoom in" by limiting our view to the first 1,000 observations:

plot_ecg(waveform_to_plot,first_n=1000)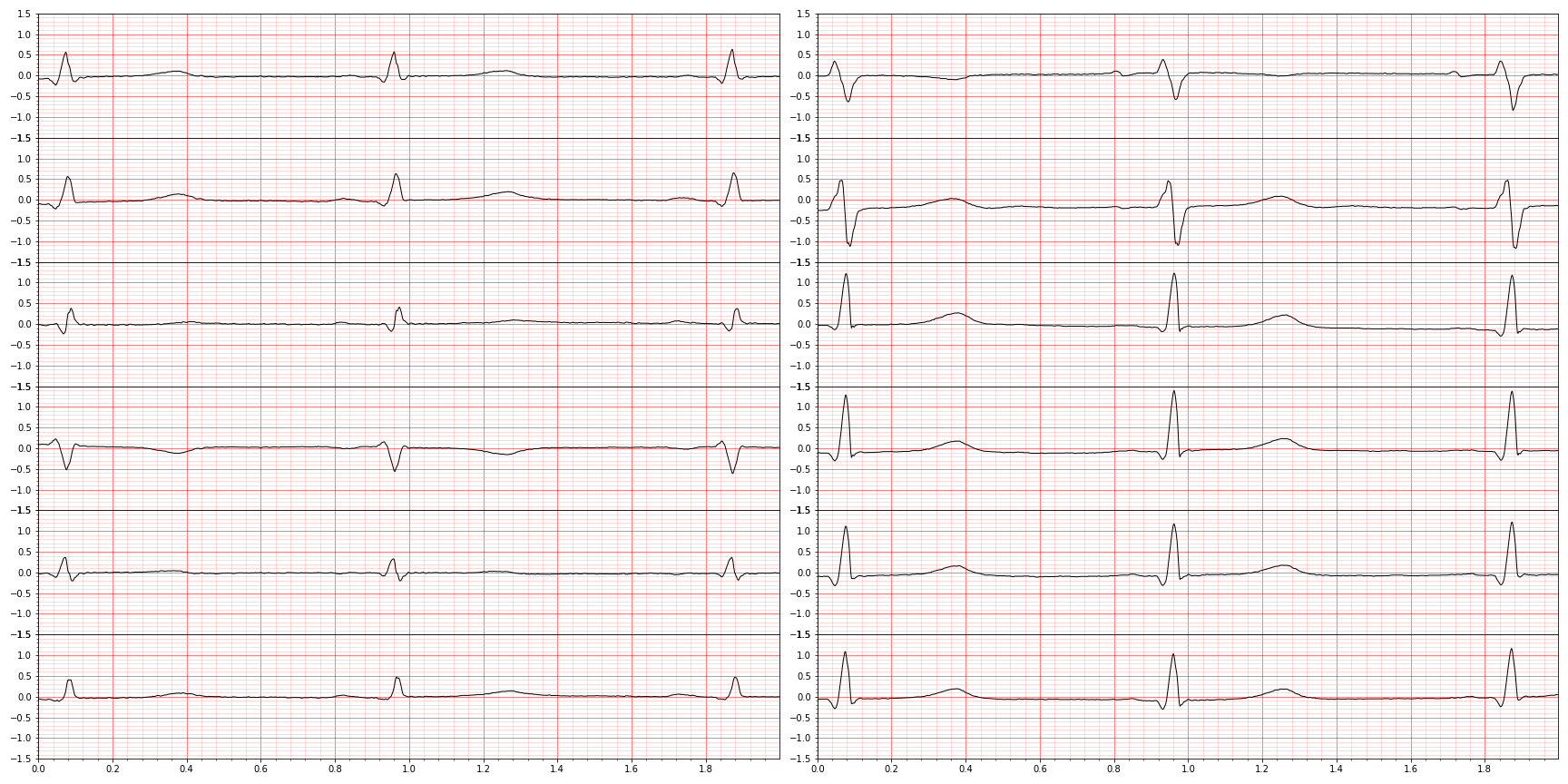

Let's have a look at the matching hea file for a mat file. In contrast to the waveforms, these header files are stored as straight-up text. This is how it looks like

HR15477 12 500 5000 04-Jun-2020 21:57:08
HR15477.mat 16+24 1000/mv 16 0 -35 32673 0 I
HR15477.mat 16+24 1000/mv 16 0 -30 -14122 0 II
HR15477.mat 16+24 1000/mv 16 0 5 18713 0 III
HR15477.mat 16+24 1000/mv 16 0 32 -9063 0 aVR
HR15477.mat 16+24 1000/mv 16 0 -20 -25175 0 aVL
HR15477.mat 16+24 1000/mv 16 0 -12 -30007 0 aVF
HR15477.mat 16+24 1000/mv 16 0 55 -19972 0 V1
HR15477.mat 16+24 1000/mv 16 0 -65 -20169 0 V2
HR15477.mat 16+24 1000/mv 16 0 0 -22967 0 V3
HR15477.mat 16+24 1000/mv 16 0 -135 -7729 0 V4
HR15477.mat 16+24 1000/mv 16 0 -75 -3951 0 V5
HR15477.mat 16+24 1000/mv 16 0 -70 -1870 0 V6
#Age: 55
#Sex: Female
#Dx: 39732003,426177001,426783006
#Rx: Unknown
#Hx: Unknown
#Sx: Unknown

with columns separated by spaces. We can break down this into three parts:

1. The first line tells us the name — which is invariantly the same as the file with the suffix removed — followed by number of leads, the sampling frequency, the number of ticks, followed by a date field.
2. The next twelve lines are the structured representation of the twelve leads with some associated meta data. We won't care about any of this, with the exception of the lead order.
3. The final six lines contains information about the participant and the diagnosis associated with this particular ECG. This is the most important and essential to get right or all downstream analyses will be worthless.

We can read this into three different data frames with three different calls to read_csv by either: 1) reading only a certain number of rows nrows, or 2) skipping some number of rows skiprows and then ignoring lines starting with a certain character comment. Don't be confused, even though the subroutine is called read_csv, you are free to choose the separator character sep.

part1 = pd.read_csv(hea_files[24291],nrows=1,header=None,sep=' ')
# >>> part1
# 	0	1	2	3	4	5
# 0	HR15477	12	500	5000	04-Jun-2020	21:57:08

part2 = pd.read_csv(hea_files[24291], skiprows=1, comment='#', sep=' ', header=None)
# >>> part2
# 0	HR15477.mat	16+24	1000/mv	16	0	-35	32673	0	I
# 1	HR15477.mat	16+24	1000/mv	16	0	-30	-14122	0	II
# 2	HR15477.mat	16+24	1000/mv	16	0	5	18713	0	III
# 3	HR15477.mat	16+24	1000/mv	16	0	32	-9063	0	aVR
# 4	HR15477.mat	16+24	1000/mv	16	0	-20	-25175	0	aVL
# 5	HR15477.mat	16+24	1000/mv	16	0	-12	-30007	0	aVF
# 6	HR15477.mat	16+24	1000/mv	16	0	55	-19972	0	V1
# 7	HR15477.mat	16+24	1000/mv	16	0	-65	-20169	0	V2
# 8	HR15477.mat	16+24	1000/mv	16	0	0	-22967	0	V3
# 9	HR15477.mat	16+24	1000/mv	16	0	-135	-7729	0	V4
# 10	HR15477.mat	16+24	1000/mv	16	0	-75	-3951	0	V5
# 11	HR15477.mat	16+24	1000/mv	16	0	-70	-1870	0	V6

part3 = pd.read_csv(hea_files[24291], skiprows=part1.shape[0]+part2.shape[0], sep=' ', header=None)
# >>> part3
# 0	#Age:	55
# 1	#Sex:	Female
# 2	#Dx:	39732003,426177001,426783006
# 3	#Rx:	Unknown
# 4	#Hx:	Unknown
# 5	#Sx:	Unknown

Let's collect these for all the 88,253 records using list-comprehension. Starting with part 1, this might take a minute or so depending on your computer:

part1_df = pd.concat([pd.read_csv(hea,nrows=1,header=None,sep=' ') for hea in hea_files],axis=0)
part1_df.columns = ['name','n_leads', 'sampling_frequency', 'n_observations', 'datetime', 'time']
# >>> part1_df
# 	name	n_leads	sampling_frequency	n_observations	datetime	time
# 0	A2112	12	500	5000	12-May-2020	12:33:59
# 0	A4563	12	500	5000	12-May-2020	12:33:59
# 0	A0705	12	500	5000	12-May-2020	12:33:59
# 0	A6374	12	500	5000	12-May-2020	12:33:59
# 0	A6412	12	500	5000	12-May-2020	12:33:59
# ...	...	...	...	...	...	...
# 0	I0055	12	257	462600	15-May-2020	15:42:19
# 0	I0041	12	257	462600	15-May-2020	15:42:19
# 0	I0040	12	257	462600	15-May-2020	15:42:19
# 0	I0054	12	257	462600	15-May-2020	15:42:19
# 0	I0068	12	257	462600	15-May-2020	15:42:19

All the names are unique and all the waveforms have 12 leads, so we don't need to worry about that. Don't take my word for it? Check it out yourself? How would you do that? We can see that there are many different lengths though

pd.unique(part1_df.n_observations)
# array([  2500,   3000,   4000, ..., 118184, 120012, 462600])

In fact, there are 1,969 different lengths. Knowing this will become important later. Also there are three different sampling frequencies available.

pd.unique(part1_df.sampling_frequency)
# array([ 500, 1000,  257])

This is also important information that we will have to address later.

How about part 2? Following the same approach as above:

part2_df = pd.concat([pd.read_csv(hea, skiprows=1, comment='#', sep=' ', header=None) for hea in hea_files],axis=0)
# >>> part2_df
# 	0	1	2	3	4	5	6	7	8
# 0	A2112.mat	16+24	1000/mV	16	0	-70	-2	0	I
# 1	A2112.mat	16+24	1000/mV	16	0	-56	-6	0	II
# 2	A2112.mat	16+24	1000/mV	16	0	14	7	0	III
# 3	A2112.mat	16+24	1000/mV	16	0	62	8	0	aVR
# 4	A2112.mat	16+24	1000/mV	16	0	-41	46	0	aVL
# ...	...	...	...	...	...	...	...	...	...
# 7	I0068.mat	16+24	1000/mv	16	0	-579	-10333	0	V2
# 8	I0068.mat	16+24	1000/mv	16	0	1316	-2153	0	V3
# 9	I0068.mat	16+24	1000/mv	16	0	2517	-1780	0	V4
# 10	I0068.mat	16+24	1000/mv	16	0	-76	-11851	0	V5
# 11	I0068.mat	16+24	1000/mv	16	0	215	6953	0	V6

But now we have 12 different rows for the same mat file. We are interested in finding out if all the leads are ordered the same across the entire dataset. The most straightforward way to do this would be to collapse the 8th column for each mat file into a string and then look at the number of unique strings. Luckily, panda comes with some utility functions we can use. First, we group our rows by their mat name, which happens to be the column called 0, and then for each of those groupings, we apply a simple function that concatenates column 8. A lambda function is simply a fancy computer science word for "an unnamed function". Note that we simply inline this little function directly without first defining it like normal (with def).

lead_orders = part2_df.groupby(0).apply(lambda grp: ','.join(grp[8]))
# >>> lead_orders
# 0
# A0001.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# A0002.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# A0003.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# A0004.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# A0005.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
#                               ...                  
# S0545.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# S0546.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# S0547.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# S0548.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# S0549.mat    I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6
# Length: 88253, dtype: object

We can now look at how many unique strings there are.

pd.unique(lead_orders)
# array(['I,II,III,aVR,aVL,aVF,V1,V2,V3,V4,V5,V6'], dtype=object)

Luckily, all the ECGs in this dataset have the same lead order, namely I, II, III, aVR, aVL, aVF, V1-V6.

We don't really care about any other information in the part 2 data frame. So let's move on to part 3. Construction into a data frame proceed with list comprehension as for the other parts. Then we give our columns some human-readable names.

part3_df = pd.DataFrame([pd.read_csv(hea, skiprows=13, sep=' ', header=None, names=['row',hea])[hea] for hea in hea_files])
# Give our columns some human-readable names
part3_df.columns = ['Age','Sex','Dx','Rx','Hx','Sx']
# >>> part3_df
# 	Age	Sex	Dx	Rx	Hx	Sx
# WFDB_CPSC2018/A2112.hea	55	Male	426783006	Unknown	Unknown	Unknown
# WFDB_CPSC2018/A4563.hea	44	Female	426783006	Unknown	Unknown	Unknown
# WFDB_CPSC2018/A0705.hea	92	Male	270492004	Unknown	Unknown	Unknown
# WFDB_CPSC2018/A6374.hea	51	Male	59118001	Unknown	Unknown	Unknown
# WFDB_CPSC2018/A6412.hea	36	Male	164884008	Unknown	Unknown	Unknown
# ...	...	...	...	...	...	...
# WFDB_StPetersburg/I0055.hea	74	Male	425856008,164865005	Unknown	Unknown	Unknown
# WFDB_StPetersburg/I0041.hea	66	Male	266257000,427393009,164884008	Unknown	Unknown	Unknown
# WFDB_StPetersburg/I0040.hea	66	Male	266257000,11157007,164884008,164930006	Unknown	Unknown	Unknown
# WFDB_StPetersburg/I0054.hea	74	Male	251182009,425856008,164865005,164884008	Unknown	Unknown	Unknown
# WFDB_StPetersburg/I0068.hea	62	Male	164884008,74390002	Unknown	Unknown	Unknown

We should rename our index such that it matches the keys we defined above — simply removing the *.hea extension in this case.

part3_df.index = [idx.split('.')[0] for idx in part3_df.index]

Ok so let's think about what we need for our classification task. We need the diagnosis labels for each ECG, which is exactly what we have here. But can we feed comma-separated strings to our deep learning model? Can we even construct a model without knowing how many unique labels there are? No and no. Luckily, the PhysioNet dataset comes with two additional files that you may have noticed in the beginning: dx_mapping_scored.csv and dx_mapping_unscored.csv. Let's combine these two dataframes together.

# Scored diagnosis lookups
dx_lookup = pd.read_csv('dx_mapping_scored.csv')

# Set the index to be the `SNOMEDCTCode` column
dx_lookup = dx_lookup.set_index('SNOMEDCTCode')

# Set these to be graded
dx_lookup['graded'] = 1

# Read the ungraded diagnosis lookups
dx_lookup2 = pd.read_csv('dx_mapping_unscored.csv')

# Set the index to be the `SNOMEDCTCode` column
dx_lookup2 = dx_lookup2.set_index('SNOMEDCTCode')

# Set these to be ungraded
dx_lookup2['graded'] = 0

# Concatenate these two together
dx_lookup = pd.concat([dx_lookup, dx_lookup2])

# >>> dx_lookup
# 	Dx	Abbreviation	CPSC	CPSC_Extra	StPetersburg	PTB	PTB_XL	Georgia	Chapman_Shaoxing	Ningbo	Total	Notes	graded
# SNOMEDCTCode													
# 164889003	atrial fibrillation	AF	1221	153	2	15	1514	570	1780	0	5255	NaN	1
# 164890007	atrial flutter	AFL	0	54	0	1	73	186	445	7615	8374	NaN	1
# 6374002	bundle branch block	BBB	0	0	1	20	0	116	0	385	522	NaN	1
# 426627000	bradycardia	Brady	0	271	11	0	0	6	0	7	295	NaN	1
# 733534002	complete left bundle branch block	CLBBB	0	0	0	0	0	0	0	213	213	We score 733534002 and 164909002 as the same d...	1
# ...	...	...	...	...	...	...	...	...	...	...	...	...	...

The Dx column in part3_df map to the SNOMEDCTCode column in this diagnosis table. This is also helpful because we can immediately see that there are 133 rows. In short, the SNOMED Clinical Term (CT) codes are computer-understandable medical terms. We are going to construct a reverse lookup table such that each diagnosis maps to all the ECGs that have been classified with that diagnosis. As a concrete example, {'atrial fibrillation': ['WFDB_CPSC2018/A4205', 'WFDB_CPSC2018/A6360', 'WFDB_CPSC2018/A2106']} tells us that these three ECGs have been classified to have atrial fibrillation. Let's run this for all the samples

# Map diagnoses to subjects using a simple dictionary.
dx_map = {}
# Foreach row in `part3_df`
for i, dat in part3_df.iterrows():
    # Split `Dx` string using a comma delimiter. Then loop over
    # each of those substrings/tokens and update our diagnosis map
    for dx in [int(x) for x in dat['Dx'].split(',')]:
        # Look up this row in the `dx_lookup` dataframe and grab the
        # `Dx` value there.
        key = dx_lookup.loc[dx]['Dx']
        # Append the current row name if the list is not empty
        # otherwise store as a new list.
        if key in dx_map: dx_map[key].append(dat.name)
        else: dx_map[key] = [dat.name]

Printing this becomes messy, so we can clean this up by counting the number of ECGs per label using dictionary comprehension. The peculiar looking [*dx_map] is a shorthand for retrieving the keys from a dictionary as a list.

dx_map_counts = {x: len(dx_map[x]) for x in [*dx_map]}

Finally, we can sort this summarized dictionary using built-in sorted functionality in Python by telling it to sort by the second item in descending order using a lambda function.

dict(sorted(dx_map_counts.items(), key=lambda item: -item[1]))
# {'sinus rhythm': 28971,
#  'sinus bradycardia': 18918,
#  't wave abnormal': 11716,
#  'sinus tachycardia': 9657,
#  'atrial flutter': 8374,
#  'left axis deviation': 7631,
#  'myocardial infarction': 6144,
#  'left ventricular high voltage': 5401,
#  'atrial fibrillation': 5255,
#  's t changes': 5009,
#  'nonspecific st t abnormality': 4712,
#  'left ventricular hypertrophy': 4406,
#  't wave inversion': 3989,
#  'sinus arrhythmia': 3790,
# ...

We can also plot these numbers but that's not necessary or particularly useful unless you're giving a presentation. Here are the top-25 most frequent diagnostic labels.

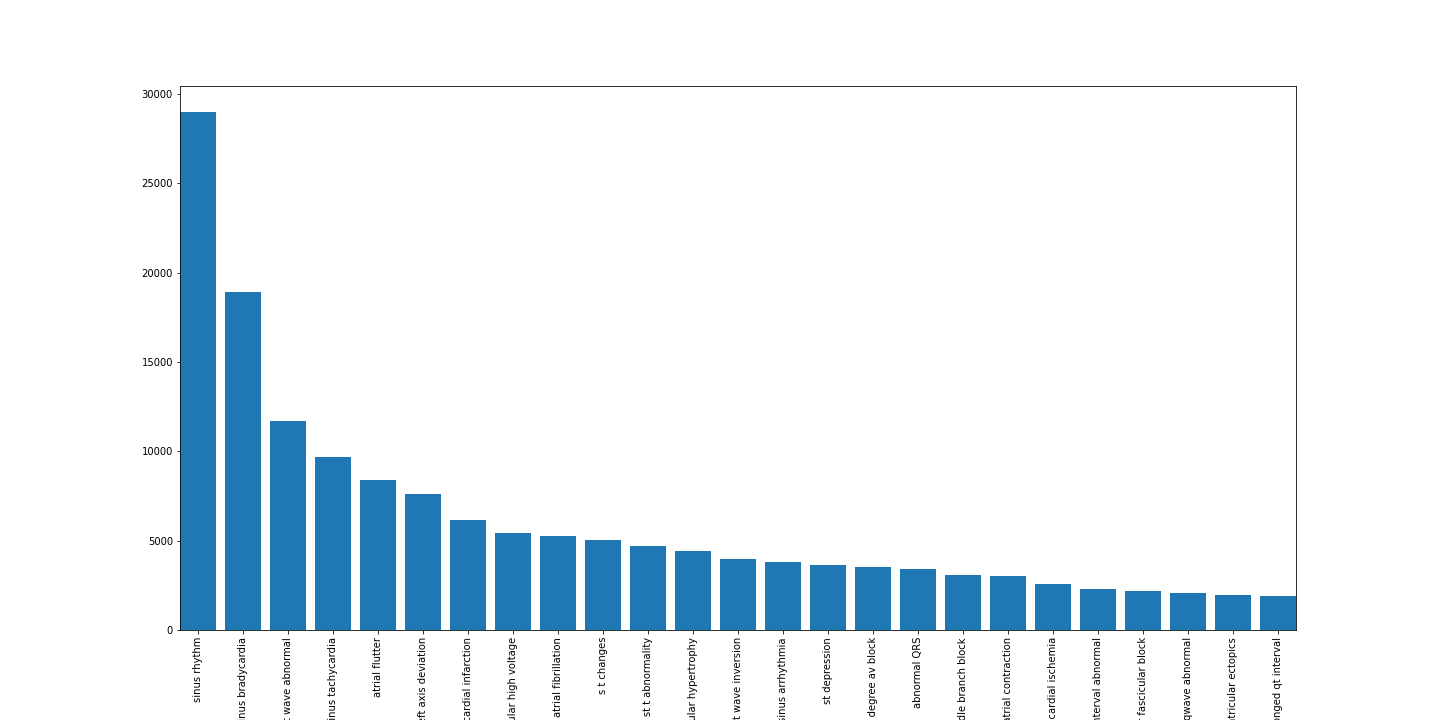
Lets also randomly plot an ECG for each diagnosis:

# For each key in our reverse lookup dictionary
for key in [*dx_map]:
    # Load a random waveform with that disease label
    waveform_to_plot = np.array(scipy.io.loadmat(dx_map[key][np.random.randint(0,len(dx_map[key])-1,1)[0]] + '.mat')['val'])
    # Restrict what we plot to the first 5,000 data points
    if waveform_to_plot.shape[-1] > 5000:
        plot_ecg(waveform_to_plot,first_n=5000)
    else:
        plot_ecg(waveform_to_plot)

    # Save the plotted file to disk and remove spaces with underscores
    key = key.replace(' ','_')
    plt.savefig(f'physionet_{key}.png')
    plt.close()

and we end up with something like this (showing nine random diagnoses)

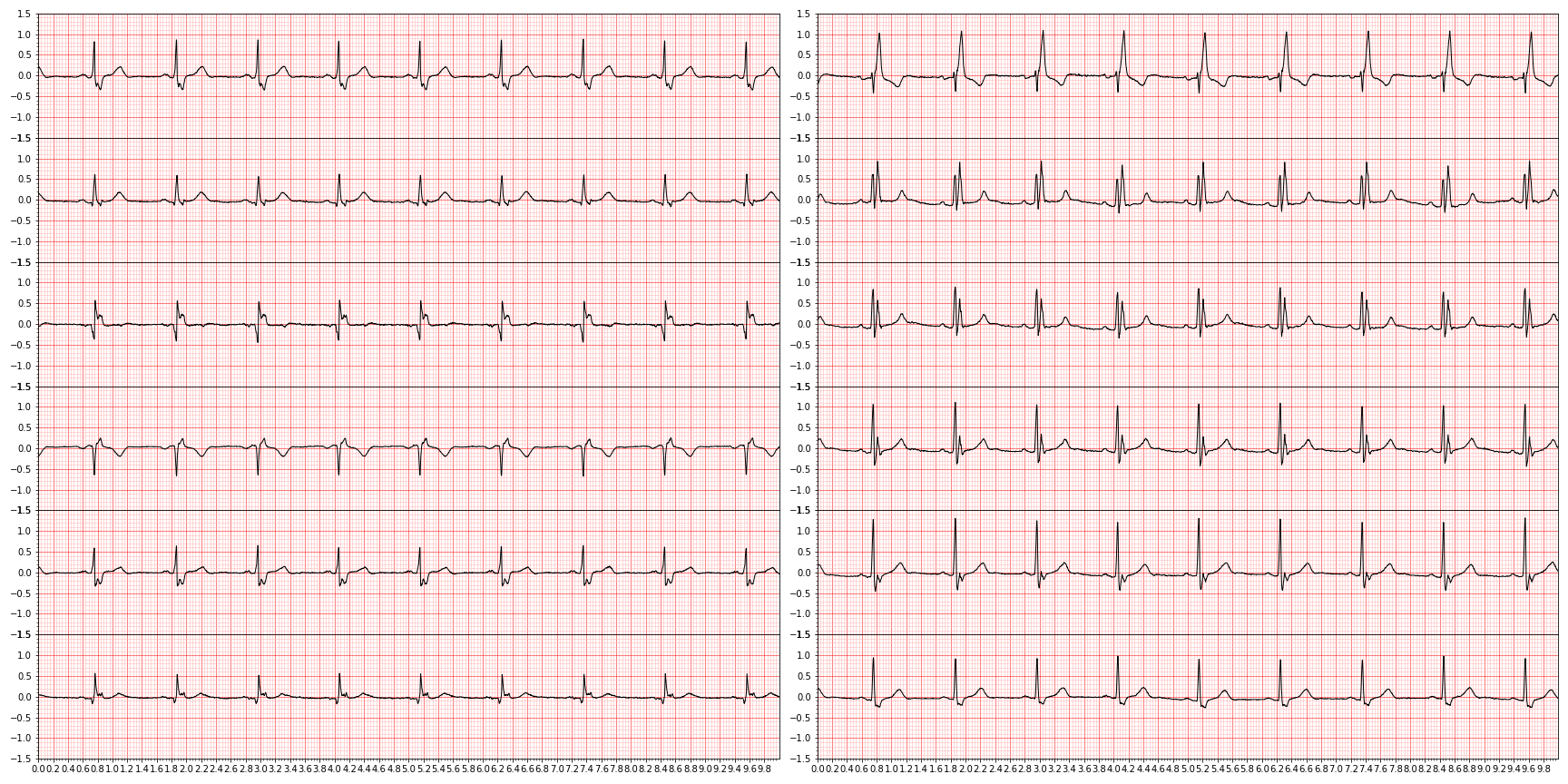
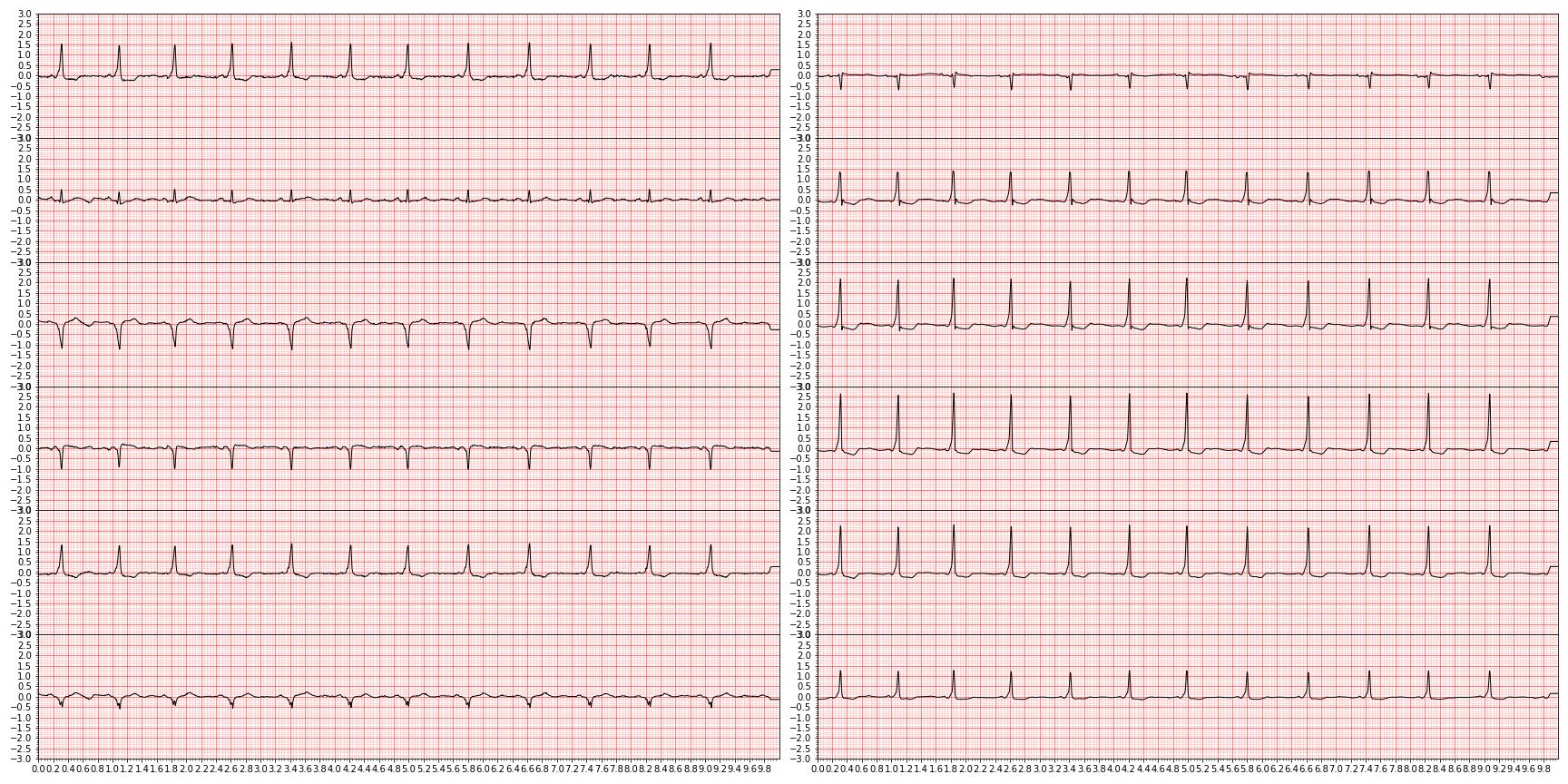
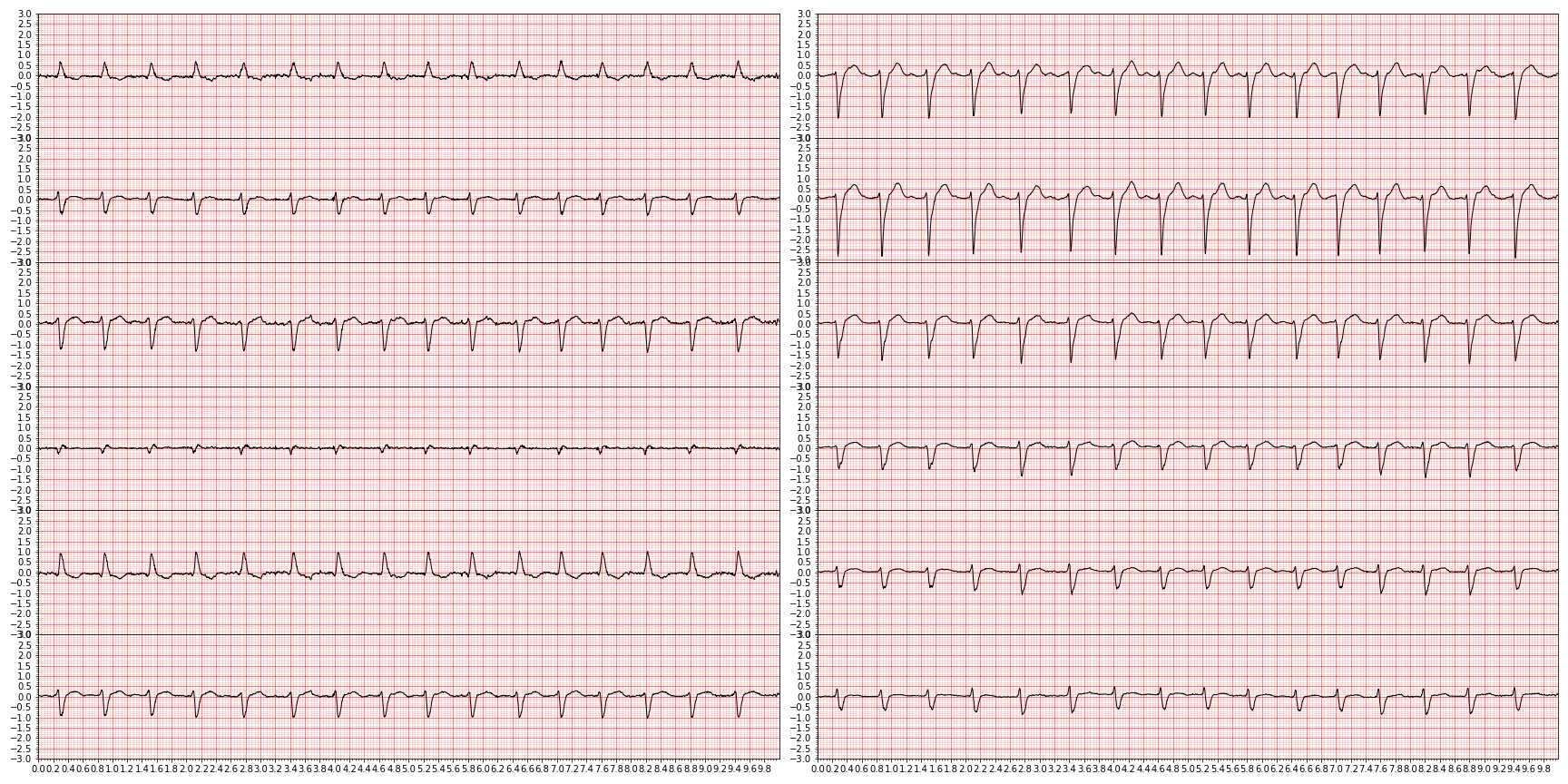
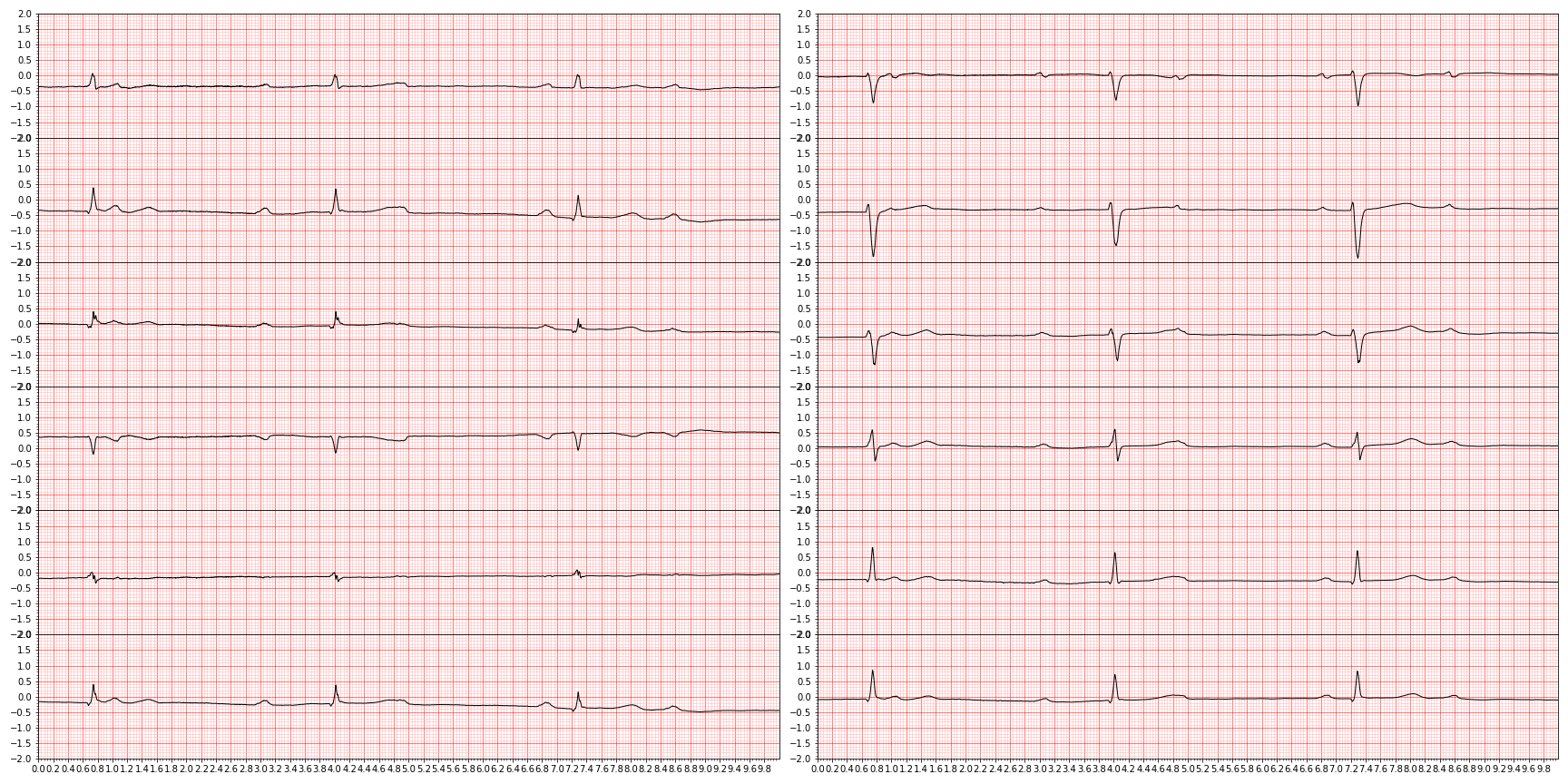
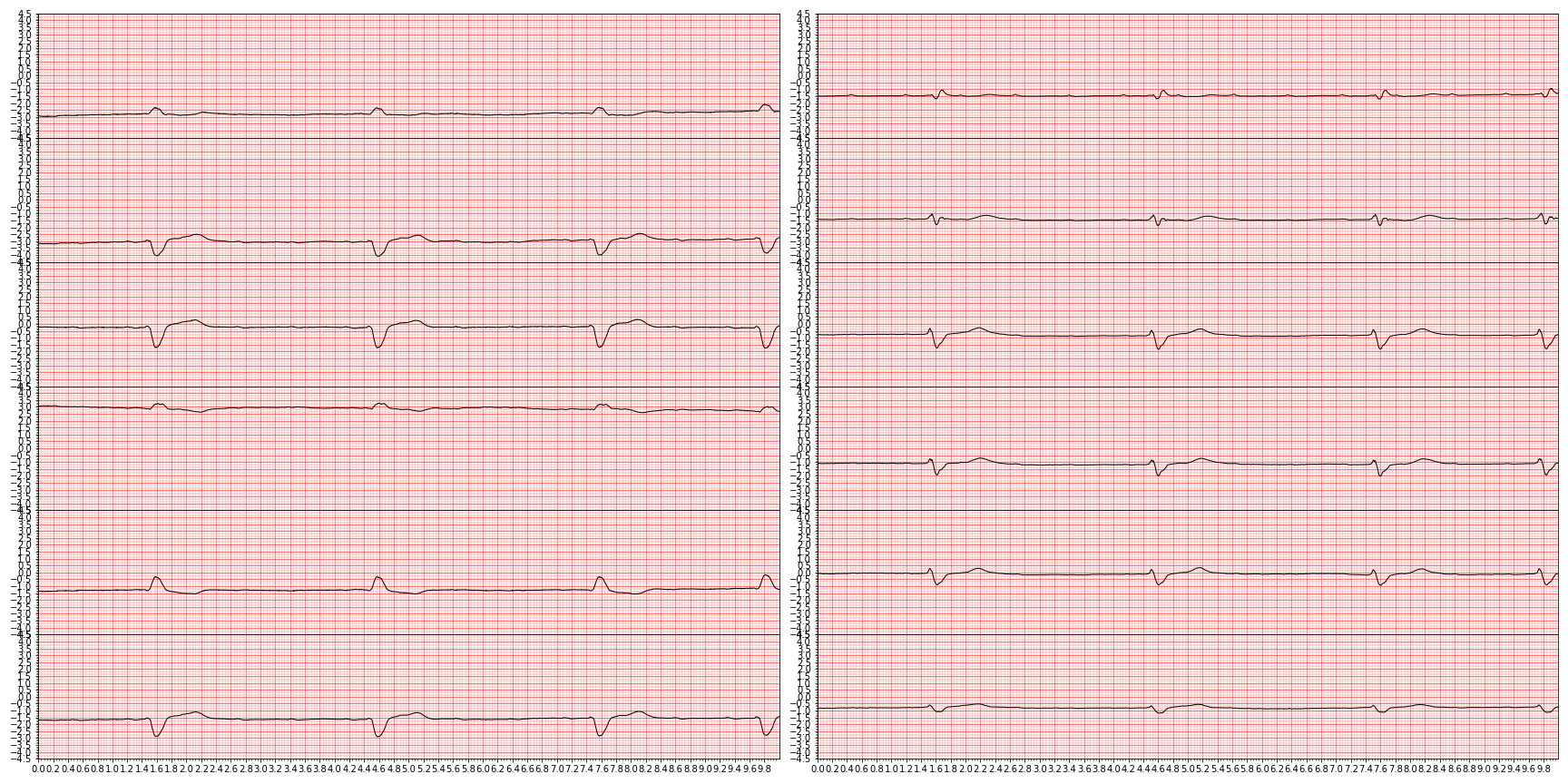
For downstream tasks, we're only interested in those diagnoses that are actually graded in the PhysioNet challenge, so let's focus only on those by slicing them out.

dx_graded = dx_lookup[dx_lookup.graded==1]

Before we prepare the final diagnosis labels, we can see that the Notes column describe a few cases where two diagnosis classes are collapsed — or rather graded as the same diagonsis. For example: We score 733534002 and 164909002 as the same. So the scored classes are actually fewer than there are rows in this table. Since we want to compare apples-to-apples performance metrics, we too, will preprocess our diagnosis labels to use this reduced/collapsed list.

pd.unique(dx_graded.Notes)
# array([nan, 'We score 733534002 and 164909002 as the same diagnosis',
#        'We score 713427006 and 59118001 as the same diagnosis.',
#        'We score 284470004 and 63593006 as the same diagnosis.',
#        'We score 427172004 and 17338001 as the same diagnosis.'],
#       dtype=object)

In order to keep the original SNOMEDCTCode column for possible downstream analyses, we will copy this column into remap. Then, one of the two equally scored diagnosis labels will then be forced into the other label. For example, we will set 164909002 to 733534002. Repeating this for the other four instances, we will end up with:

# Make a copy of the data frame
dx_graded_collapsed = dx_graded.copy()
# Reset the index to 0..n
dx_graded_collapsed = dx_graded_collapsed.reset_index()
# Copy the column `SNOMEDCTCode` and call it `remap`
dx_graded_collapsed['remap'] = dx_graded_collapsed['SNOMEDCTCode']
# Replace the `SNOMEDCTCode` codes that a graded equally with one or the other
dx_graded_collapsed.loc[dx_graded_collapsed.SNOMEDCTCode==164909002,'remap'] = 733534002
dx_graded_collapsed.loc[dx_graded_collapsed.SNOMEDCTCode==59118001, 'remap'] = 713427006
dx_graded_collapsed.loc[dx_graded_collapsed.SNOMEDCTCode==63593006, 'remap'] = 284470004
dx_graded_collapsed.loc[dx_graded_collapsed.SNOMEDCTCode==427172004,'remap'] = 17338001
# >>> dx_graded_collapsed
# SNOMEDCTCode	Dx	Abbreviation	CPSC	CPSC_Extra	StPetersburg	PTB	PTB_XL	Georgia	Chapman_Shaoxing	Ningbo	Total	Notes	graded	remap
# 0	164889003	atrial fibrillation	AF	1221	153	2	15	1514	570	1780	0	5255	NaN	1	164889003
# 1	164890007	atrial flutter	AFL	0	54	0	1	73	186	445	7615	8374	NaN	1	164890007
# 2	6374002	bundle branch block	BBB	0	0	1	20	0	116	0	385	522	NaN	1	6374002
# 3	426627000	bradycardia	Brady	0	271	11	0	0	6	0	7	295	NaN	1	426627000
# 4	733534002	complete left bundle branch block	CLBBB	0	0	0	0	0	0	0	213	213	We score 733534002 and 164909002 as the same d...	1	733534002
# 5	713427006	complete right bundle branch block	CRBBB	0	113	0	0	542	28	0	1096	1779	We score 713427006 and 59118001 as the same di...	1	713427006
# 6	270492004	1st degree av block	IAVB	722	106	0	0	797	769	247	893	3534	NaN	1	270492004
# 7	713426002	incomplete right bundle branch block	IRBBB	0	86	0	0	1118	407	0	246	1857	NaN	1	713426002

We can now map each unique diagnosis label to a unique counting number 0, 1, 2, etc. using dictionary comprehension.

# Map each unique `remap` code to a unique number
graded_lookup = {k: i for i,k in enumerate(pd.unique(dx_graded_collapsed.remap))}
# >>> graded_lookup
# {164889003: 0,
#  164890007: 1,
#  6374002: 2,
#  426627000: 3,
#  733534002: 4,
#  713427006: 5,
# ...

As a sanity check, we then verify that some SNOMEDCTCode indeed have non-unique mappings

graded_lookup = {k: graded_lookup[a] for k,a in zip(dx_graded_collapsed.SNOMEDCTCode,dx_graded_collapsed.remap)}
# >>> graded_lookup

We are now finally ready to prepare the diagnosis labels for each ECG. There are two principal ways we approach this:

1. Prepare the labels as one-hot encoded vectors and store those directly, or
2. Prepare the labels as the graded_lookup mappings and compute the one-hot encodings on-the-fly at training time

It is generally good practice to go for the second choice as this requires less memory and disk space, especially for very large datasets and/or for very many labels. In this case, either option works equally well.

Proceeding with option 2, we simply loop over our data frame as before and map the SNOMEDCTCode to our counting values using the graded_lookup dictionary.

# The ECG->diagnosis label dictionary
graded_category_map = {}

# For each row in the meta data frame
for i in range(part3_df.shape[0]):
    graded_dx_patient = []
    # Strip white spaces and then split each string into list of keys
    for a in part3_df.Dx[i].strip().split(','):
        # If the key exists in the list of keys we are interested in:
        if int(a) in graded_lookup.keys():
            # Append the mapping index for that key
            graded_dx_patient.append(graded_lookup[int(a)])
    
    # Store all the keys for each person in a dictionary
    graded_category_map[part3_df.index.values[i]] = {'dx_labels': graded_dx_patient}
    
# >>> graded_category_map
# {'WFDB_CPSC2018/A2112': {'dx_labels': [12]},
#  'WFDB_CPSC2018/A4563': {'dx_labels': [12]},
#  'WFDB_CPSC2018/A0705': {'dx_labels': [6]},
#  'WFDB_CPSC2018/A6374': {'dx_labels': [5]},
#  'WFDB_CPSC2018/A6412': {'dx_labels': []},
#  'WFDB_CPSC2018/A0063': {'dx_labels': []},
#  'WFDB_CPSC2018/A4205': {'dx_labels': [0]},
#  'WFDB_CPSC2018/A2674': {'dx_labels': []},
#  'WFDB_CPSC2018/A4211': {'dx_labels': [5]},
#  'WFDB_CPSC2018/A2660': {'dx_labels': [12]},
#  'WFDB_CPSC2018/A6406': {'dx_labels': [5]},
#  'WFDB_CPSC2018/A1369': {'dx_labels': [5]},
#  'WFDB_CPSC2018/A0077': {'dx_labels': []},
#  'WFDB_CPSC2018/A0711': {'dx_labels': [12]},
#  'WFDB_CPSC2018/A6360': {'dx_labels': [0, 5]},
#    ...

Let us check the distribution of the number of diagnoses per ECG

# Count how many diagnosis there are per ECG
graded_category_map_counts = np.array(np.unique([len(v['dx_labels']) for k,v in graded_category_map.items()],return_counts=True))
# >>> graded_category_map_counts
# array([[    0,     1,     2,     3,     4,     5,     6,     7,     8],
#        [ 6287, 49815, 20981,  8020,  2411,   583,   128,    25,     3]])

Because we restricted out attention to only the graded diagnoses labels, we have some ECGs without a label — 6,287 to be exact. We will simply remove these using dictionary comprehension by adding a condition in the end:

# Remove people who have no labels for the diagnoses we are interested in
graded_category_map_nonzero = {k: v for k, v in graded_category_map.items() if len(v['dx_labels'])}

This brings us down from 88,253 to 81,966, which is around 8% fewer.

As a final note on performance, we ended up reading the same 80k files three times — once for part 1, once for part2, and once for part 3. This is definitely not the most efficient. If we were to write this in a production setting, we process each file three times while still in memory. But that approach would be less instructional.

So from the data exploration we have learned:

1. The ECG waveforms have different lengths but are always 12 leads, in the same lead order, and have different sampling rates
2. There are 26 unique diagnoses labels we are interested in
3. There are 6,287 ECGs without a diagnosis label that we care about

Now when we have finished exploring and preparing the meta data and diagnosis labels, let's move on to ingesting, compressing, and storing the actual ECG waveforms. First, let's save our files.

Saving files and best practices

It is a very good practice to 1) track changes you make with a version control tool like Git and 2) make sure that you don't accidentally overwrite larger files as these are normally not versioned. How to use Git is outside the scope of this tutorial. Every time you run a notebook or script you want to make sure that you don't corrupt or change existing files with the same base name. The easiest way to guarantee this won't happen is to use the package uuid that provides functions to generate Universally Unique IDentifiers (UUIDs) — or random names in our use-case. More specifically, we will use version 4 UUIDs, and you definitely don't need to understand how this works. Luckily, this is very straightforward

# Generate a version 4 UUID and convert it to a hexanumeric
# string representation
version_hash = uuid.uuid4().hex
# >>> version_hash
# '1df07a0b2c1a422d9141d8951dacb38a'

and now we can combine this unique string with our regular output names. For example, let's combine the meta data into a single joint data frame and save this to disk for downstream applications.

# Concatenate `part3_df` and `part1_df` side-by-side (axis=1)
# We also set the index of `part1_df` to that of `part3_df` since we know
# they are indeed in the same order and thus share the same index
meta_data = pd.concat([part3_df, part1_df.set_index(part3_df.index)], axis=1)
# The output name for the file we want to write to disk
output_name = 'KLARQVIST_physionet__meta_data__' + version_hash + '.csv'
# Write data to a csv file
meta_data.to_csv(output_name)

Remember that our meta data dataframe contains ECGs without a diagnosis label we are interested in. We can just remove to and save this second dataframe

# Keep only ECGs for which we have a valid diagnosis label
meta_data_graded = meta_data.loc[[*graded_category_map_nonzero]]
# The output name for the file we want to write to disk
output_name = 'KLARQVIST_physionet__meta_data_graded__' + version_hash + '.csv'
# Write data to a csv file
meta_data_graded.to_csv(output_name)

Let's also save our dictionaries to disk with pickle for downstream analyses. In short, the pickle module can convert Python objects into a byte stream which we can write to disk, and reciprocally, restore a Python object from disk. We need to open a file handle with open and declare that we would like to write w and that it is binary b.

# The destination directory is the current directory
destination = './'
# Write our dictionaries as binary `pickle` objects to disk
X_train.to_csv(os.path.join(destination,'KLARQVIST_physionet__meta_data__train__' + version_hash + '.csv'))
pickle.dump(graded_category_map, open(os.path.join(destination,'KLARQVIST_physionet__diagnosis_labels__' + version_hash + '.pickle', 'wb'))
pickle.dump(graded_category_map_nonzero, open(os.path.join(destination,'KLARQVIST_physionet__diagnosis_labels_nonzero__' + version_hash + '.pickle', 'wb'))

We now have all the diagnostic labels prepared and easily queryable. We are now ready to move on to ingesting and processing the ECG waveforms themselves.

Ingesting and compressing the ECG waveforms

There are 88,253 waveforms with matching header files in this dataset. We definitely don't want to keep working with 176,506 separate files all the time. Not only is that annoying, but it is also not particularly efficient. We can reduce all the files into two files:

1. The structured meta data and diagnosis information, and
2. A single archive with the compressed waveforms

We've already built up our structured data using pandas. For the ECG waveforms, there are a bunch of approaches we can take to compress and store these. For this tutorial, I've decided to use the HDF5 archive format for the simple reason that it is very widely used and so gaining experience with this file format is time well spent.

In a nutshell, the HDF5 format is a way to organize data, in a fashion that is equivalent to folders on your computer, with one or more files in a folder and with the possibility of adding some additional descriptive information called "attributes". As a concrete example, we can store the value 5 at the path /path/to/my/number. Accessing datasets and attributes is then trivial with hdf5['/path/to/my/number'] to retrieve a pointer to the data. That's all we need to care about for this tutorial, and in fact, this is true for the vast majority of real-world applications as well.

As we noted while building up the meta data, and what is described in the PhysioNet challenge text, all but two of the ECG datasets are sampled at 500 Hz. For the other two, we will either downsample from 1,000 Hz or upsample from 257 Hz. In order to downsample from 1,000 to 500 Hz, all we need to do is to simply ignore every second data point. That's it. For upsampling, we will take advantage of the scipy function called zoom. Don't be confused by the function name, it simply performs an interpolation between our lower frequency waveform and a target higher frequency one. After any potential processing of the waveforms, we will then simply compress and store them in the HDF5 archive. Why we chose this compression doesn't really matter for understanding and that discussion is outside the scope of this tutorial.

import scipy # For loading and upsampling waveform data
import h5py # For HDF5

# The destination directory is the current directory
destination = './'
# The output name for the HDF5 archive we write to disk
# We will resuse the same `version_hash` as before
output_name = 'KLARQVIST_physionet__waveforms__' + version_hash + '.h5'

# With this new HDF5 file as `writef`. This syntax will automatically close the file handle
# and flush when the loop ends.
with h5py.File(os.path.join(destination,output_name), "w") as writef:
    # Loop over each row in our `dat_files` data frame
    # `i`` is an incremental counter, and `dat` is the `Series` (i.e. row) at offset `i``.
    for i, dat in dat_files.iterrows():
        # Load an ECG waveform from disk using the `loadmat` function in scipy. This
        # is simply how the organizers of the PhysioNet challenge decided to store them.
        local = np.array(scipy.io.loadmat(dat['mat'])['val'])
        
        # The St Peterburg dataset is sampled at 257 Hz, unlike the 500 Hz for most
        # of the other datasets. We will simply resample from 257 to 500 Hz. We will
        # "cheat" a bit and use the `zoom` functionality in scipy.
        if dat['src'] == 'WFDB_StPetersburg':
            local = scipy.ndimage.zoom(local, (1,500/257))
        # The PTB dataset is sampled at 1000 Hz which is twice that of the other
        # datasets. We can downsample to 500 Hz by selecting every second data point.
        elif dat['src'] == 'WFDB_PTB':
            local = local.copy()[0:len(local):2] # Downsample to 500 Hz
        
        # Force C-order for Numpy array
        local = np.asarray(local, order='C')
        
        # Use some aggressive compression to store these waveforms. We can achieve
        # around 2.8 - 3-fold reduction in size, with a small decompression cost,
        # with these settings.
        compressed_data = blosc.compress(local, typesize=2, cname='zstd', clevel=9, shuffle=blosc.SHUFFLE)
        
        # Store the compressed data.
        dset = writef.create_dataset(dat['key'], data=np.void(compressed_data))
        # Store the shape as meta data for the dataset
        dset.attrs['shape'] = local.shape

Running this might take 60 min or more depending on your machine. If this was for production, and not education, we would speed up this with multiprocessing. However, I feel that multiprocessing is a separate beast that is well outside the scope of this tutorial. Read one of my other tutorials while you wait. Ok, fine, I will provide a prepared example to parallelize this — but discussion of what is going on really is outside the scope of this tutorial.

First, we simply wrap a function definition around the above snippet (excluding the imports) and call that ingest_ecg_worker(dat_files). Because of weird multiprocessing rules in Python, we have to save this function together with all the imports in a separate file. Let's call this multiprocessing_ecg.py. We only need to make one modification: we want to generate a unique UUID for each worker in order to make sure that each worker writes to different files.

def ingest_ecg_worker(dat_files):
    # Construct a "random" name for our archive.
    version_hash = uuid.uuid4().hex
    # The destination directory is the current directory
    destination = './'
    # The output name for the HDF5 archive we write to disk
    output_name = 'KLARQVIST_physionet__waveforms__' + version_hash + '.h5'
    ...

Now we can simply type import multiprocessing_ecg and we have our module with that function available to us.

Next, we have to describe another function that splits our dataset into chunks and then lets each processor/thread asynchronously compute all the ECGs in that chunk. I will just leave this commented snippet here and move on.

from multiprocessing import Pool, cpu_count
import time
import multiprocessing_ecg


def multiprocess_ingest_ecgs(
    files,
):
    # Split our list of files into N number of roughly equally sizes lists, where
    # N is the number of CPUs available on your machine.
    split_files = np.array_split(files, cpu_count())
    # Print a nice message
    print(f'Beginning ingesting {len(files)} ECGs using {cpu_count()} CPUs.')
    # Start a timer --- this way we can measure how long processing took.
    start = time.time()
    # With a multiprocessing pool, we asynchronously call our function `_ingest_ecgs` N
    # number of times --- one per CPU thread. Each thread will be given a different subset
    # of the available files.
    with Pool(cpu_count()) as pool:
        results = [pool.apply_async(multiprocessing_ecg.ingest_ecg_worker, (split,)) for split in split_files]
        for result in results:
            result.get()
    # Measure how long time processing took.
    delta = time.time() - start
    # Print a nice message
    print(f'Projections took {delta:.1f} seconds at {delta / len(files):.1f} s/ECG')

Running this as multiprocess_ingest_ecgs(dat_files)now finishes in Projections took 918.6 seconds at 0.01 s/ECG on my 8 core / 16 thread Macbook laptop. But we now have 16 different HDF5 files, or however many threads you have on your computer, so we need to merge these in another loop.

# The destination directory is the current directory
destination = './'
# The output name for the HDF5 archive we write to disk
output_name = 'KLARQVIST_physionet__waveforms__' + version_hash + '__combined.h5'

# With this new HDF5 file as `writef`. This syntax will automatically close the file handle
# and flush when the loop ends.
with h5py.File(os.path.join(destination,output_name), "w") as writef:
    # Loop over all the partial files.
    for part in partial_hdf5_files:
        # Read the partial file
        with h5py.File(part, 'r') as f:
            keys = [] # Keep track of the keys/paths
            level1 = list(f) # List the dataset names
            for l in level1: # Foreach dataset name, list the datasets
                keys += [l + '/' + k for k in list(f[l])]
            for k in keys: # Iterate over keys and copy over
                # This will also take care of the attributes
                f.copy(f[k], writef, k)

You can now safely remove the partial files. We now have all the ECG waveforms compressed and stored in a single file.

Prepare train-test-validation splits

When training machine learning models, we almost always need to split our data into three chunks:

1. The training data we use to update our model weights
2. The testing data we use to evaluate how well our model is doing and when to stop training
3. The held out validation data on which we evaluate the actual model performance

There are of course other partitioning paradigms such as K-fold cross-validation, but these kinds of approaches are less frequently used in deep learning as they are considerably more expensive to evaluate.

There are a bunch of way we can split our data, but the easiest is undoubtfully to use the scikit package and the provided train_test_split function.

from sklearn.model_selection import train_test_split

Lets have a look at what it does by feeding it the sequence of numbers $0, 1, ..., 99$. We will also tell the function to first shuffle our data (shuffle) in a deterministic fashion (random_state) and return 20% as testing data and the remaining 80% as training data. Note that we can set the random_state of the random number generator to any integer, all of which give different results, albeit reproducibly. I decided to use 1337 because that number is part of computer history.

train_test_split(np.arange(100), test_size=0.2, shuffle=True, random_state=1337)
# [array([10, 73, 76, 53, 52, 31, 25, 94,  5, 80, 37, 16, 40, 21, 55, 49, 83,
#         77, 78, 45,  0, 33, 12, 13, 28, 69, 64, 35, 58,  7, 47, 74, 29, 85,
#         62, 38, 14, 71,  4, 42, 34, 41,  3, 26, 18, 93, 46, 97, 68, 95, 98,
#          8, 20, 67, 57, 51, 19, 60, 65, 75, 66, 22, 88, 27,  1, 24, 99, 54,
#          6,  9, 72, 84, 82, 90, 96, 89, 39, 92, 61, 23]),
#  array([ 2, 48, 86, 44, 59, 56, 79, 70, 91, 17, 50, 32, 36, 87, 15, 11, 63,
#         81, 30, 43])]

As expected, we are returned two lists, one with 80 values and another with 20 values. If we provided train_test_split with both an X and y value, we will get four lists back: the train and test splits for X and the train and test splits for y:

train_test_split(np.arange(100), np.arange(1000,1100), test_size=0.2, shuffle=True, random_state=1337)
# [array([10, 73, 76, 53, 52, 31, 25, 94,  5, 80, 37, 16, 40, 21, 55, 49, 83,
#         77, 78, 45,  0, 33, 12, 13, 28, 69, 64, 35, 58,  7, 47, 74, 29, 85,
#         62, 38, 14, 71,  4, 42, 34, 41,  3, 26, 18, 93, 46, 97, 68, 95, 98,
#          8, 20, 67, 57, 51, 19, 60, 65, 75, 66, 22, 88, 27,  1, 24, 99, 54,
#          6,  9, 72, 84, 82, 90, 96, 89, 39, 92, 61, 23]),
#  array([ 2, 48, 86, 44, 59, 56, 79, 70, 91, 17, 50, 32, 36, 87, 15, 11, 63,
#         81, 30, 43]),
#  array([1010, 1073, 1076, 1053, 1052, 1031, 1025, 1094, 1005, 1080, 1037,
#         1016, 1040, 1021, 1055, 1049, 1083, 1077, 1078, 1045, 1000, 1033,
#         1012, 1013, 1028, 1069, 1064, 1035, 1058, 1007, 1047, 1074, 1029,
#         1085, 1062, 1038, 1014, 1071, 1004, 1042, 1034, 1041, 1003, 1026,
#         1018, 1093, 1046, 1097, 1068, 1095, 1098, 1008, 1020, 1067, 1057,
#         1051, 1019, 1060, 1065, 1075, 1066, 1022, 1088, 1027, 1001, 1024,
#         1099, 1054, 1006, 1009, 1072, 1084, 1082, 1090, 1096, 1089, 1039,
#         1092, 1061, 1023]),
#  array([1002, 1048, 1086, 1044, 1059, 1056, 1079, 1070, 1091, 1017, 1050,
#         1032, 1036, 1087, 1015, 1011, 1063, 1081, 1030, 1043])]

Let's think about what we need to partition:

1. The ECG waveforms, and
2. The diagnostic labels

Both are accessible with the same key: source folder/file. So all we really need to split into train, test, and validation is the list of available keys! However, in order to be educational, and to observe what happens to the distribution of diagnostic labels if we randomly partition data, let's prepare the one-hot encoded vectors and pass those along too.

One-hot encoding is a fancy way of saying that we want to have a vector of zeros with length equal to the number of unique classes with the $k$-th element set to as one. So for example, given the classes banana, shoes, and bobsled, and an ECG with the label shoes, we would first construct a vector of three zeros [0,0,0] and then set the second value (corresponding to shoes) to 1, resulting in [0,1,0]. In cases where there are multiple class labels per ECG, we simply keep setting the appropriate values to 1. For example, there is an ECG with shoes and bobsled which would then have the one-hot vector [0,1,1]. Importantly for this next section, note this can be interpreted as the sum of the shoes and bobsled one-hot vectors: [0,1,0] + [0,0,1] = [0,1,1]. This is then known as a multi-hot vector.

Since we will be using TensorFlow and Keras in the second part, let's use the provided tf.one_hot function. For demonstrative purposed, let's look at

# An ECG with eight (8) diagnosis labels
graded_category_map_nonzero['WFDB_Ningbo/JS20289']['dx_labels']
# [13, 18, 23, 10, 25, 19, 24, 16]

and see what happens if we compute one-hot encodings with TensorFlow

# We have 26 unique diagnostic labels, see above
tf.one_hot(graded_category_map_nonzero['WFDB_Ningbo/JS20289']['dx_labels'], 26)
# <tf.Tensor: shape=(8, 26), dtype=float32, numpy=
# array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.,
#         0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#         0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#         0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.,
#         0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#         0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#         0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#         0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
#        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
#         1., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)>

Woot woot? We get a tensor of shape (8,26) back. If we look closely, we can see that we get one one-hot encoded vector back for each label even though they all belong to the same ECG. As mentioned above, the sum of all individual one-hot vectors will be the multi-hot vector. So all we need to do is to sum columnwise across these vectors.

# Compute the one-hot vectors as above and then sum
# columnwise (0th axis)
tf.reduce_sum(tf.one_hot(graded_category_map_nonzero['WFDB_Ningbo/JS20289']['dx_labels'], 26), axis=0)
# <tf.Tensor: shape=(26,), dtype=float32, numpy=
# array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 1., 0., 0., 1.,
#        0., 1., 1., 0., 0., 0., 1., 1., 1.], dtype=float32)>

And now we have the desired result! TensorFlow always return tf.Tensors but for our exercise we just want vanilla Numpy. We can always convert back to Numpy by calling .numpy() on any TensorFlow tensor. We can now produce all the multi-hot vectors for all the ECGs using list comprehension — as we've seen multiple times already.

one_hot_labels = np.array([tf.reduce_sum(tf.one_hot(x['dx_labels'],26), axis=0).numpy() for x in graded_category_map_nonzero.values()])

Putting this together, we then split into 80% training data and 20% remainder which we in turn then split into 50/50 for test and validation:

# First split keys and one-hot labels into 80% train and 20% remaining
X_train, X_remainder, y_train, y_remainder = train_test_split(
    meta_data_graded.index.values, 
    one_hot_labels, 
    test_size = 0.2, # 0.8 and 0.2
    shuffle=True, 
    random_state=1337)
# Then we split the remaining 20% into 50% meaning 10% test and 10% validation w.r.t. the original amount
X_test, X_validation, y_test, y_validation = train_test_split(
    X_remainder, 
    y_remainder, 
    test_size = 0.5, # 0.5 out of 0.2 = 0.1 and 0.1 out of total 
    shuffle=True, 
    random_state=1337)

We can count how many diagnostic labels ended up in the train, test, and validation partitions by simply summing column-wise over the multi-hot vectors — look above for the intuition if it's not immediately obvious to you — and collect these in a data frame.

# Set the index to be the `remap` column from the
# `dx_graded_collapsed` data frame.
y_data_df = pd.DataFrame({
    'train': np.sum(y_train, axis=0)
    'test':  np.sum(y_test,  axis=0),
    'validation': np.sum(y_validation, axis=0)
}, index=pd.unique(dx_graded_collapsed.remap))
# >>> y_data_df
# 	train	test	validation
# 164889003	4197.0	556.0	502.0
# 164890007	6709.0	812.0	853.0
# 6374002	403.0	60.0	59.0
# 426627000	234.0	31.0	30.0
# 733534002	1209.0	145.0	140.0
# 713427006	3879.0	476.0	475.0
# 270492004	2821.0	336.0	377.0
# 713426002	1452.0	201.0	204.0
# 39732003	6110.0	762.0	759.0
# ...

By eyeballing these numbers, we can see that randomly shuffling and partitioning our data gives good representation of all labels across the splits. Let's compute a different statistics with respect to the training data. First, we compute the proportionality of each label within each partition by dividing each label count with the total number of examples in each partition. This is straighforward by dividing the data frame with the column-wise sums (total counts per partition).

(y_data_df / y_data_df.sum(axis=0))

This is not very easy on the eyes, so we then also divide the label counts in each partition with the count in the training data. This is also pretty straightforward by applying a lambda function in the row-wise direction.

(y_data_df / y_data_df.sum(axis=0)).apply(lambda x: x / x[0], axis=1)
# 	train	test	validation
# 164889003	1.0	1.073556	0.954653
# 164890007	1.0	0.980815	1.014781
# 6374002	1.0	1.206521	1.168498
# 426627000	1.0	1.073581	1.023261
# 733534002	1.0	0.971920	0.924235
# 713427006	1.0	0.994434	0.977360
# 270492004	1.0	0.965217	1.066643
# 713426002	1.0	1.121807	1.121358
# 39732003	1.0	1.010654	0.991474
# 445118002	1.0	0.989065	1.089004
# 251146004	1.0	0.876927	0.949441
# 698252002	1.0	0.978338	0.902297
# 426783006	1.0	1.038652	1.014668
# 284470004	1.0	1.025481	1.062343
# 10370003	1.0	1.048969	0.985862
# 365413008	1.0	0.926597	0.974477
# 17338001	1.0	1.047003	0.979633
# 164947007	1.0	0.954907	1.042162
# 111975006	1.0	0.908004	0.982171
# 164917005	1.0	0.958514	0.972648
# 47665007	1.0	1.095323	0.945890
# 427393009	1.0	0.906572	0.962963
# 426177001	1.0	0.966635	0.962501
# 427084000	1.0	1.018224	0.999747
# 164934002	1.0	0.968942	1.002663
# 59931005	1.0	0.958185	1.086780

We can immediately see that there are a bunch of labels that are not equally represented — although not too badly distributed in this case — across the partitions, in the range of ± 15% or so. Can we do better?

There is a great package for multi-label tasks called skmultilearn that provides a number of approaches to reduce this variability in labels across partitions. We will be using iterative_train_test_split as an illustrative example.

from skmultilearn.model_selection import iterative_train_test_split

# `iterative_train_test_split` would like to have the input `X` values as arrays,
# we therefore use list comprehension to simply wrap each element into a list.
# Also note that `iterative_train_test_split` returns lists as `x`,`y`,`x`,`,y`
# unlike `train_test_split` that returns lists as `x`,`x`,`y`,`y`, for train and
# test respectively.
X_train, y_train, X_remainder, y_remainder = iterative_train_test_split(
    np.array([[x] for x in meta_data_graded.index.values]),
    one_hot_labels, 
    test_size = 0.2,) # 0.8 and 0.2

X_test, y_test, X_validation, y_validation = iterative_train_test_split(
    X_remainder, 
    y_remainder, 
    test_size = 0.5,) # 0.5 out of 0.2 = 0.1 and 0.1 out of total 

The syntax is very similar with a few differences highlighted in the code. Let's rerun our proportional statistics and see if we observe any improvements in the distribution of labels across partitions.

y_data_df = pd.DataFrame({
    'train': np.sum(y_train, axis=0),
    'test':  np.sum(y_test,  axis=0),
    'validation': np.sum(y_validation, axis=0)
}, index=pd.unique(dx_graded_collapsed.remap))

(y_data_df / y_data_df.sum(axis=0)).apply(lambda x: x / x[0], axis=1)
	train	test	validation
# 164889003	1.0	0.989103	0.995412
# 164890007	1.0	0.990784	0.994021
# 6374002	1.0	0.985308	0.989708
# 426627000	1.0	0.973264	1.011321
# 733534002	1.0	0.987559	0.998627
# 713427006	1.0	0.997226	0.997558
# 270492004	1.0	0.988994	0.996225
# 713426002	1.0	0.991377	0.990451
# 39732003	1.0	0.989883	0.994303
# 445118002	1.0	1.040001	0.971657
# 251146004	1.0	0.990819	0.995244
# 698252002	1.0	1.076718	0.973940
# 426783006	1.0	0.990002	0.994423
# 284470004	1.0	0.988529	0.995989
# 10370003	1.0	0.989209	0.993627
# 365413008	1.0	0.990045	0.963389
# 17338001	1.0	1.045118	0.967449
# 164947007	1.0	0.990045	1.045464
# 111975006	1.0	0.986152	0.995769
# 164917005	1.0	1.109143	1.119004
# 47665007	1.0	0.990045	0.994466
# 427393009	1.0	0.990045	0.994466
# 426177001	1.0	0.990176	0.994597
# 427084000	1.0	0.990301	0.993694
# 164934002	1.0	1.022119	1.016442
# 59931005	1.0	1.063778	1.076125

We can immediately see that almost all the labels are equally represented across the partitions, in the range of ± 1% or so. A big improvement! In some cases, especially for rare labels, the difference can be huge!

Let's save the X splits to disk and wrap up the preprocessing. Note that we don't care about the y values (multi-hot encoded values) as we will compute these on-the-fly during training. Instead of just saving the lookup keys as a list of strings, I think it's nicer to save all the relevant meta data instead — even though you can easily produce this with the keys. Since iterative_train_test_split returns X as a list-of-lists, we will have to flatten these into a single contiguous list by calling .ravel(). Then we simply slice out the rows with the matching key name using .loc().

X_train = meta_data.loc[X_train.ravel()]
X_test  = meta_data.loc[X_test.ravel()]
X_validation = meta_data.loc[X_validation.ravel()]

We then write these to disk, reusing the same version_hash we've been using all along.

# The destination directory is the current directory
destination = './'
# Write out data frames to disk as `csv` files
X_train.to_csv(os.path.join(destination,'KLARQVIST_physionet__meta_data__train__' + version_hash + '.csv'))
X_test.to_csv(os.path.join(destination,'KLARQVIST_physionet__meta_data__test__' + version_hash + '.csv'))
X_validation.to_csv(os.path.join(destination,'KLARQVIST_physionet__meta_data__validation__' + version_hash + '.csv'))

We are now ready with the preprocessing steps! Huzzah!

Conclusions

This concludes the first part of this tutorial. We have learned 1) how to download PhysioNet-2021 ECG data, 2) how to explore and preprocess diagnostic labels, and 3) plotting and preparing ECG waveforms in the HDF5 format, 4) partitioning diagnostic labels into train, test, and validation in a balanced fashion. In the next part of this tutorial, we will start building simple convolutional neural network models to classify ECGs according to these diagnostic labels.